N°09-2025
Enunciado
Sean $U = {(\theta, \varphi) \in \mathbb{R}^2 : -\pi/2 \leq \theta \leq \pi/2 \text{ y } 0 \leq \varphi \leq 2\pi}$ y $\overline{F}: U \to \mathbb{R}^3$ dada por
$$ \overline{F}(\theta, \varphi) = (\cos \theta \cos \varphi, \cos \theta \sin \varphi, C \sin \theta), $$
donde $C$ es una constante positiva. En lo que sigue, llamaremos superficie del planeta a la superficie dada por la imagen de $F$ y mapa al conjunto $U$.
a) Describir la superficie del planeta mediante una ecuación en coordenadas cartesianas (de la forma $f(x, y, z) = 0$). Graficar el planeta para $C = 1/2$.
b) ¿Verdadero o falso? Para $C = 1$, si $A_1$ y $A_2$ son dos regiones del mapa que tienen igual área entonces, en el planeta, las áreas de las regiones que representan (es decir, de las regiones $\overline{F}(A_1)$ y $\overline{F}(A_2)$) también son iguales. Justificar la respuesta.
Resolución
a)
Si definimos $\overline{F} \equiv (x,y,z)$, podemos pensar la parametrización coordenada a coordenada:
$$ \begin{split} \overline{F}(\theta, \varphi) &= (x (\theta ,\varphi),y (\theta ,\varphi), z(\theta ,\varphi)) \\ &= (\cos \theta \cos \varphi, \cos \theta \sin \varphi, C \sin \theta) \end{split} $$
de manera que, dejando atrás la notación funcional:
$$ \begin{cases} x &= \cos \theta \cos \varphi \\ y &= \cos \theta \sin \varphi \\ z &= C \sin \theta \end{cases} $$
Las coordenadas $x$ y $y$ tienen a $\cos \theta$ como factor común, pero a su vez dependen del coseno y el seno de $\varphi$. Elevando al cuadrado y sumando, podemos eliminar la dependencia en $\varphi$. Luego, podemos tratar de independizarnos de $\theta$ recurriendo a su dependencia con $z$:
$$ \begin{split} x^2+y^2 &= \cos^2 \theta \cos^2 \varphi + \cos^2 \theta \sin^2 \varphi \\ &= \cos^2 \theta (\cos^2 \varphi +\sin^2 \varphi) \\ &= \cos^2 \theta \\ &= 1 - \sin^2 \theta \\ &= 1 - \left( \frac{z}{C} \right)^2 \end{split} $$
finalmente obtenemos la siguiente dependencia implícita
$$ \boxed{x^2+y^2 +\left( \frac{z}{C} \right)^2 = 1} $$
que representa un elipsoide de semiejes $1$, $1$ y $C$ en las coordenas $x$, $y$ y $z$, respectivamente.
Si $C=1/2$, el elipsoide será “achatado” en la dirección $z$ e isométrico en los ejes $x$ y $y$ (Figura A).
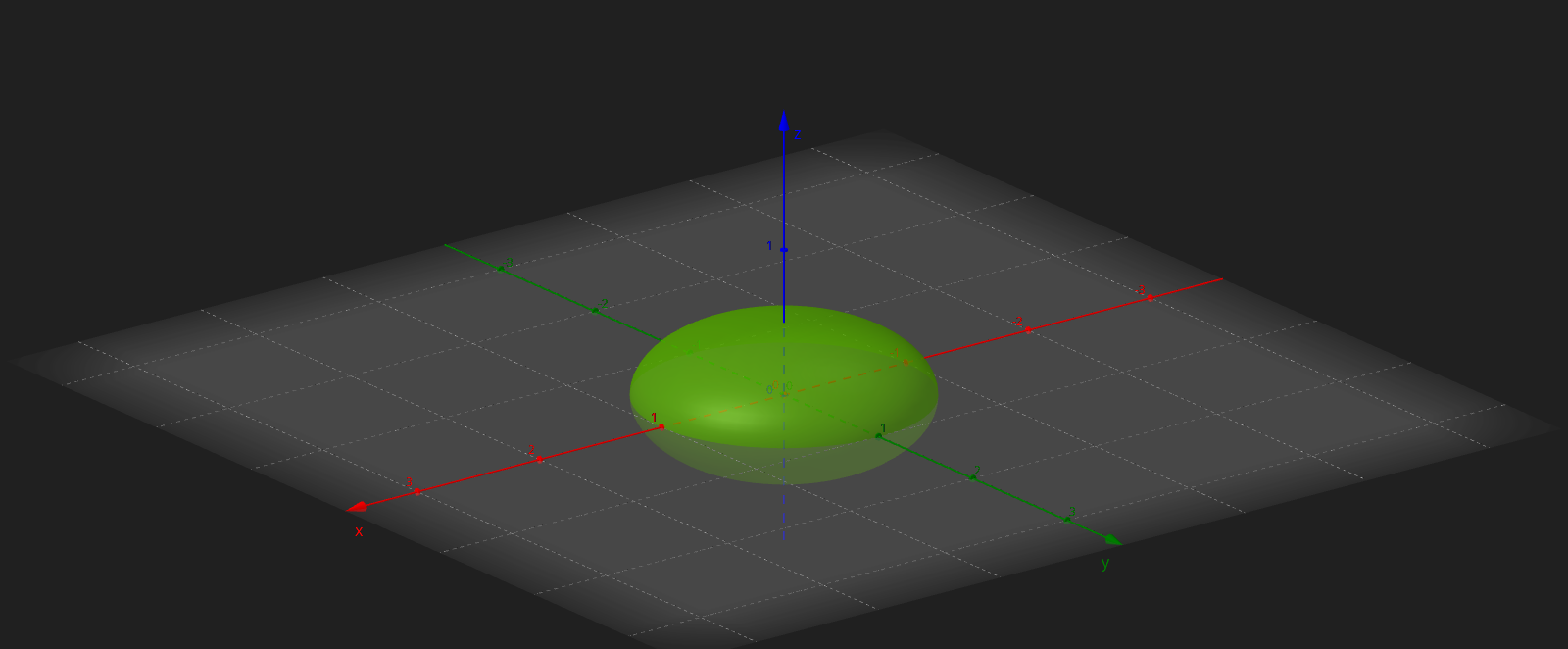
Figura A
b)
Con las manos
Para $C=1$ la superficie es esférica.
Los cartógrafos saben muy bien que las superficies sobre la esfera terrestre no mantienen su proporcionalidad en un mapa plano. Entenderemos a qué se debe al desarrollar la respuesta a este inciso. Comencemos dándonos cuenta que un mapa plano común y corriente, como el que usamos en nuestras clases de geografía, son un mapa cartesiano de los ángulos respecto del ecuador y del meridiano de Greenwich. Es decir, podemos usar los ángulos $(\theta,\varphi)$, lo cuál da sentido denominar mapa al conjunto $U$.
Luego, pensemos en una franja de tamaño $\Delta \varphi$ en el mapa. Sobre tal franja, podemos imaginar diferentes rectángulos de área $\Delta \varphi \Delta \theta$ o, para ponerle más dinámica a la idea, podemos imaginar un mismo rectángulo trasladándose por la franja. ¿Cómo se vería la franja y este «movimiento» dentro de ella?
Como $\theta \in \left[ - \frac{\pi}{2}, \frac{\pi}{2}\right]$, la franja de ancho $\Delta \varphi$ es una «rodaja» como la representada en (Figura B1).

Figura B1
Ahora consideremos dos rectángulos en el mapa $U$ de igual área $\Delta\theta \Delta\varphi$, ubicadas en diferentes latitudes:
- uno centrado en el ecuador ($\theta = 0$);
- otro centrado cerca del polo norte ($\theta \approx \pi/2$).
Sus imágenes en la esfera (Figura B2) son regiones delimitadas por meridianos ($\varphi$ constante) y paralelos ($\theta$ constante). La longitud de los arcos de paralelo es proporcional a $\cos\theta$ (el radio de los paralelos es $\cos \theta$). Por lo tanto, la región cercana al polo tiene una extensión longitudinal menor que la del ecuador, aunque en el mapa tengan la misma área. Esto sugiere (no demuestra) que la afirmación es falsa: áreas iguales en el mapa no corresponden necesariamente a áreas iguales en el planeta.

Para ayudar a la imaginación, les dejo la siguiente animación donde se observan las diferentes imágenes de los rectángulos de igual área a lo largo de una franja en el mapa .
Con saco y corbata
Para demostrar la falsedad de la afirmación, podemos recordar que el elemento de superficie (en un sentido vectorial) de la imagen de una parametrización $\overline{F}(\theta, \varphi)$ está dada por
$$ d \overline{s} = (\overline{F}_{\theta} \times \overline{F}_{\varphi}) d\theta d \varphi $$
donde $\overline{F}_{\theta} = \frac{\partial \overline{F}}{\partial \theta}$ y $\overline{F}_{\varphi} = \frac{\partial \overline{F}}{\partial \varphi}$. Así, una superficie elemental en el mapa, de área $dA=|d\theta || d \varphi|$, generará una superficie elementa $d \overline{s}$ de área
$$ d s= ||\overline{F}_{\theta} \times \overline{F}_{\varphi}|| dA. $$
Para que cualquier superficie del mapa de área $dA$ genere la misma superficie $ds$ es necesario que el factor de escala $||\overline{F}_{\theta} \times \overline{F}_{\varphi}||$ sea independiente de $\theta$ y $\varphi$. Veamos que esto no sucede. Primero calculemos las derivadas
$$ \begin{cases} \overline{F}_{\theta} &= (- \sin \theta \cos \varphi, - \sin \theta \sin \varphi, \cos \theta) \\ \overline{F}_{\varphi} &= (- \cos \theta \sin \varphi, \cos \theta \cos \varphi, 0) \end{cases} $$
entonces
$$ \begin{split} \overline{F}_{\theta} \times \overline{F}_{\varphi} &= \begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \\ -\sin \theta \cos \varphi & - \sin \theta \sin \varphi & \cos \theta \\ -\cos \theta \sin \varphi & \cos \theta \cos \varphi & 0 \end{vmatrix} \\ &= \left(\cos^2 \theta \cos \varphi, -\cos^2 \theta \sin \varphi, -\sin \theta \cos \theta \cos^2 \varphi-\sin \theta \cos \theta \sin^2 \varphi \right) \\ &= \left(\cos^2 \theta \cos \varphi, -\cos^2 \theta \sin \varphi, -\sin \theta \cos \theta ( \cos^2 \varphi+ \sin^2 \varphi) \right) \\ &= \left(\cos^2 \theta \cos \varphi, -\cos^2 \theta \sin \varphi, -\sin \theta \cos \theta \right). \end{split} $$
Ahora determinemos su módulo
$$ \begin{split} || \overline{F}_{\theta} \times \overline{F}_{\varphi} ||^2 &= \cos^4 \theta \cos^2 \varphi+ \cos^4 \theta \sin^2 \varphi+\sin^2 \theta \cos^2 \theta \\ &= \cos^4 \theta (\cos^2 \varphi+ \sin^2 \varphi) +\sin^2 \theta \cos^2 \theta \\ &= \cos^4 \theta +\sin^2 \theta \cos^2 \theta \\ &= \cos^2 \theta ( \sin^2 \theta + \cos^2 \theta) \\ &= \cos^2 \theta \end{split} $$
y como $\cos \theta \geq 0$ para todo $\theta \in \left[ - \frac{\pi}{2}, \frac{\pi}{2}\right]$
$$ || \overline{F}_{\theta} \times \overline{F}_{\varphi} || = \cos \theta. $$
Es decir,
$$ d s= \cos \theta dA, $$
lo que demuestra que la proposición es falsa, ya para diferentes valores de $\theta$ dos superficies de área $dA$ pueden tener diferentes áreas en el planeta.
Si todavía no lo hiciste y valoras el trabajo, siempre estas a tiempo de hacer tu aporte libre y voluntario. ¡Gracias!