N°08-2025

Enunciado

El pez arquero tiene una estrategia muy particular para cazar insectos. Saca su boca fuera del agua y dispara con gran puntería un chorro de agua a alta presión que impacta sobre el insecto, haciéndolo caer y permitiendo su captura (ver figura). Se ha observado que el ángulo que forma el chorro con la superficie del agua es 72 grados (ángulo $\theta$ en la figura). Para posicionarse para el tiro, el pez arquero hace contacto visual con el insecto manteniendo sus ojos bajo la superficie del agua.

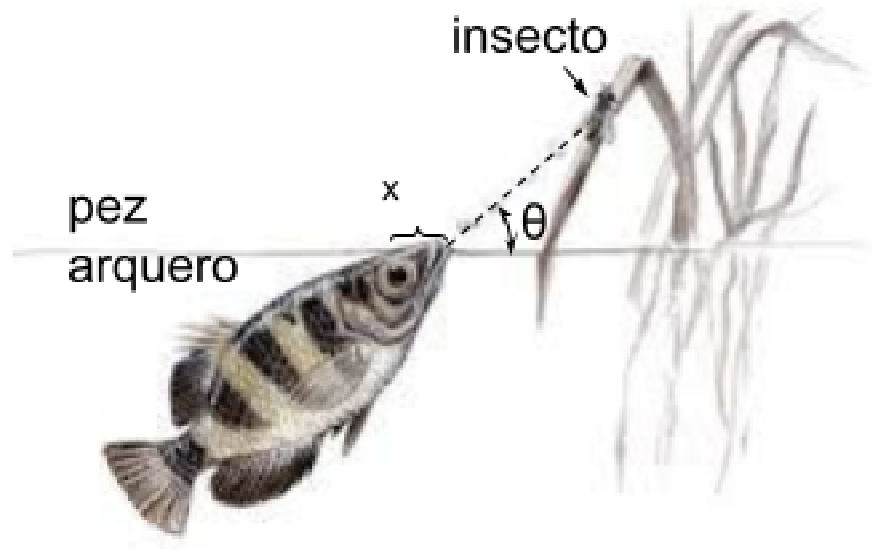
a) Despreciando la distancia $x$ entre los ojos y la boca del pez, ¿a qué ángulo respecto de la superficie del agua visualiza el pez al insecto?

b) Si no se desprecia $x$, ¿el ángulo de visión es mayor o menor que el calculado anteriormente?

Datos: el índice de refracción del agua a la temperatura ambiente es aproximadamente
$n \approx 4/3$ y el del aire $n \approx 1$.

Resolución

«El “pez arquero” (toxotes jaculator) es un ejemplar muy particular de la fauna ictícola. Consigue su alimento cazando insectos (moscas, mosquitos u otros insectos de tamaño semejante) de una forma muy curiosa. El pez, una vez que identificó su presa (detenida sobre una hoja, por ejemplo), le escupe una gota de agua de masa $m$, que hace que el insecto caiga al agua, donde se lo come.»
Problema N° 1 de las Olimpiadas Argentinas de Física en el año 2001

a)

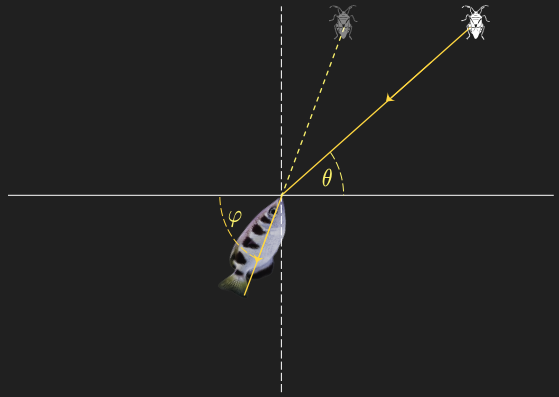
Cuando $x$ es pequeño, la dirección del chorro coincide con la dirección de la luz proveniente del insecto. Esta última, incide en la superficie del agua refractándose con un ángulo $\varphi$, respecto de ella, que estará determinado por la ley de Snell (Figura A):

$$ n \sin \left( \frac{\pi}{2} - \varphi\right) = \sin \left( \frac{\pi}{2} - \theta \right) $$

o equivalentemente

$$ n \cos \varphi = \cos \theta ~~~~~~ (1) $$

teniendo en cuenta que $n \approx 4/3$ y $\theta = 72 ^\circ$, podemos obtener que

$$ \boxed{\varphi \approx 76.6 ^\circ}. $$

b)

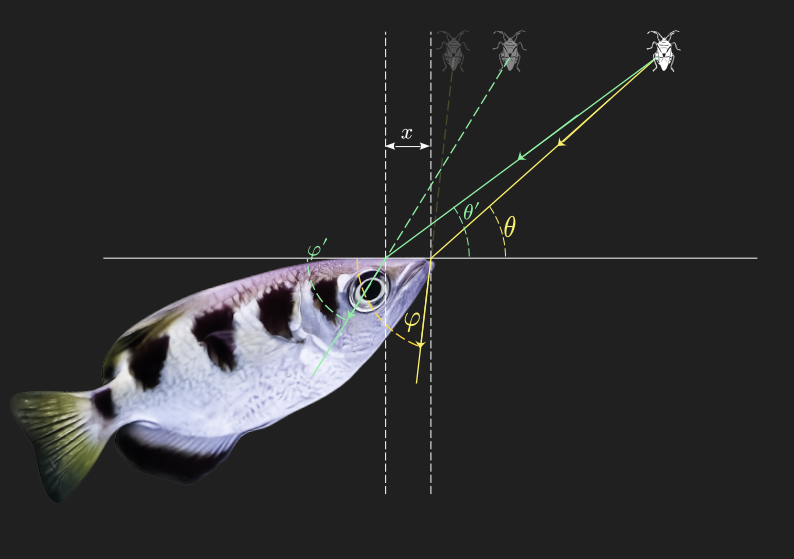
La ley de Snell, o su versión modificada expresada por la relación (1), da cuenta de la relación de monotonía creciente entre los ángulos de incidencia y refracción. Es decir, cuando un ángulo disminuye el otro también lo hace. Cuando la distancia $x$ no es nula, entonces el ángulo de incidencia $\theta’$ es menor que $\theta$. Por ello, el ángulo de refracción $\varphi’$, que coincide con el ángulo de visión del pez, será menor que el ángulo de visión $\varphi$ determinado en el inciso anterior.

Si todavía no lo hiciste y valoras el trabajo, siempre estas a tiempo de hacer tu aporte libre y voluntario. ¡Gracias!