N°05-2025

Enunciado

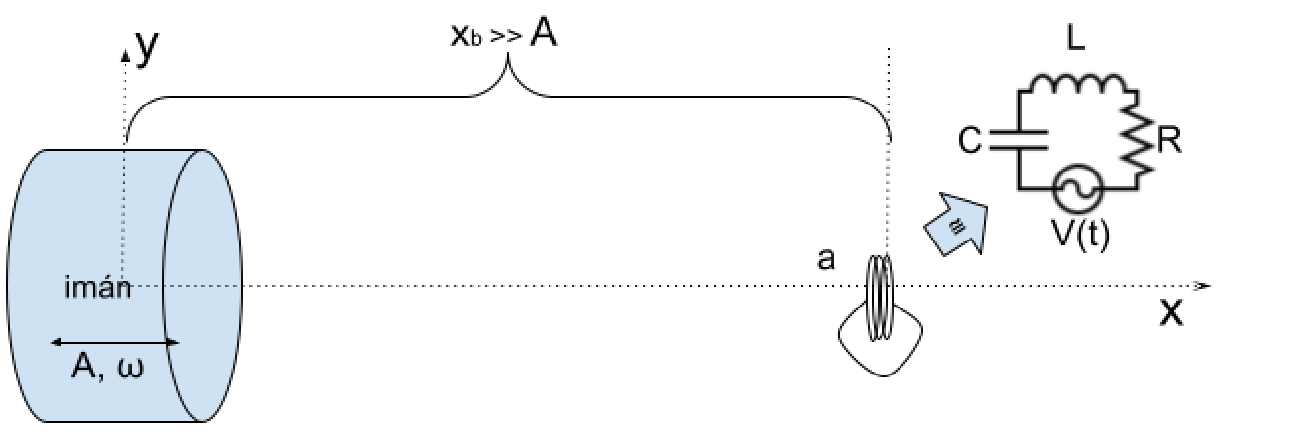
Un imán realiza oscilaciones sinusoidales forzadas en la dirección $\hat{x}$ con una frecuencia de oscilación $\omega$ y con amplitud $A$ alrededor del origen. La magnetización del imán es $\vec{M} = M \hat{x}$ y produce sobre y cerca del eje $\hat{x}$ un campo magnético:

$$ \bar{B}(x) \approx \frac{\mu_0 M / 2\pi}{(x - x_M)^3} \hat{x} $$

donde $ x_M = x_M(t) $ es la posición instantánea del centro de masa del imán respecto del origen.

Como se indica en la figura, a una distancia $ x_b \gg A$ del origen y sobre el eje $ \hat{x}$, se coloca una bobina de área $a$ y $n$ vueltas muy juntas con normal paralela al eje $\hat{x}$, y cuyos extremos están unidos. El campo magnético sobre la pequeña bobina puede considerarse uniforme y perpendicular al plano de las espiras. Se supone que la bobina real puede modelarse como un circuito ideal $RLC$ en serie, y que el voltaje $V(t)$ inducido en la bobina por el campo magnético del imán es equivalente a una fuente de tensión alterna de voltaje $V(t)$ en el circuito.

a) Mostrar que la condición $ x_b \gg A $ implica que el campo magnético uniforme sobre la bobina es aproximadamente (a primer orden en $ x_M $) sinusoidal en el tiempo. Usar esta aproximación para los siguientes cálculos.

b) Calcular $ V(t) $, para todo $ t $.

c) ¿Qué condición, en términos de $ \omega $ y de los parámetros del circuito equivalente, se tiene que dar para que el circuito $ RLC $ entre en resonancia con la perturbación oscilatoria del imán?

d) Calcular la potencia instantánea disipada en la bobina.

Resolución

a)

Desde el punto de vista funcional, el módulo campo magnético generado por la bobina en el punto $x_b$ puede considerarse dependiente de $x_M$, es decir

$$ B(x_b, x_M) \approx \frac{\mu_0 M / 2\pi}{(x_b - x_M)^3} $$

entonces, cuando $ x_b \gg A $ también $ x_b \gg x_M $ y tiene sentido realizar una aproximación hasta el primer orden del desarrollo en serie de Taylor alrededor de $0$ en la variable $x_M$:

$$ B(x_b, x_M) \approx B(x_b, 0) + \left. \frac{\partial B}{\partial x_M} \right|_{(x_b,0)} x_M. $$

Para ello, y no cargar con los factores constantes, alcanza con concentrarnos en la función

$$ b(x_M) = \frac{1}{\left( x_b - x_M\right)^3} $$

cuyo desarrollo es

$$ \begin{split} b(x_M) &\approx b(0) + b’(0) x_M \\ &\approx \frac{1}{x_b^3} + \left[ \frac{3}{\left( x_b - x_M\right)^4} \right]_{(0)} x_M \\ &\approx \frac{1}{x_b^3} +\frac{3}{ x_b^4} x_M \end{split} $$

y por lo tanto

$$ B(x_b, x_M) \approx \frac{\mu_0 M / 2\pi}{x_b^3} + \frac{3\mu_0 M / 2\pi}{x_b^4} x_M. $$

Finalmente, como el imán oscila con una frecuencia $\omega$, su posición tiene una dependencia sinusoidal con el tiempo $x_M(t) = A \sin (\omega t+\varphi)$, que explica el mismo comportamiento para el campo a grandes distancias.

$$ \boxed{B(x_b,t) \approx \frac{\mu_0 M}{2\pi x_b^3} + \frac{3\mu_0 M }{2\pi x_b^4} A \sin (\omega t+\varphi)}. ~~~~(1) $$

b)

Para determinar el voltaje inducido en la bobina, debemos obtener el flujo del campo a través de las $n$ espiras:

$$ \begin{split} \phi &= n \int_{a} \bar{B}(x_b,t) \cdot d \overline{s} \\ &= n \int_{a} (B(x_b,t) \hat{x}) \cdot (-\hat{x} da) \\ &= -n \int_{a} B(x_b,t) da \\ &= -n B(x_b,t) \int_a da \\ &= -n B(x_b,t) a
\end{split} $$

cuya derivada respecto del tiempo nos permite obtener el voltaje inducido

$$ \begin{split} V &=- \frac{d \phi}{dt}\\ &= n a \frac{d B(x_b,t)}{dt} ~~ \text{(aprovechamos la relación (1))} \\ &= n a \frac{3\mu_0 M}{2\pi x_b^4} A \omega \cos (\omega t+\varphi)\\ &= \frac{3\mu_0 M }{2\pi x_b^4} n a A \omega \cos (\omega t+\varphi) \end{split} $$

que si definimos

$$ V_0 = \frac{3\mu_0 M }{2\pi x_b^4} n a A \omega ~~~~ (2) $$

se expresa como una tensión alterna

$$ \boxed{V(t) = V_0 \cos (\omega t+\varphi)} ~~~~ (3) $$

de frecuencia $\omega$.

c)

A mi me gusta analizar los circuitos de este estilo recurriendo a los números complejos. Para ello, recuerdo que si la tensión tiene la dependencia mostrada en la relación (3), entonces la corriente tendrá una dependencia análoga pero con una fase inicial diferente:

$$ I(t) = I_0 \cos (\omega t+\varphi’) ~~~~ (4) $$

y que a partir de tales dependencias puedo construir las funciones complejas definidas como

$$ \begin{cases} \widetilde{V} (t)&= V_0 e^{i(\omega t + \phi)} \\ \widetilde{I} (t)&= I_0 e^{i(\omega t + \phi’)} \end{cases} ~~~~ (5) $$

tales que

$$ \begin{cases} V(t) &= \mathrm{Re} (\widetilde{V} (t)) ~ \land ~ V_0 = |\widetilde{V} (t)|\\ I(t) &= \mathrm{Re} (\widetilde{I} (t)) ~ ~\land ~ I_0 = |\widetilde{I} (t)|. \end{cases} $$

En este contexto es válida la siguiente generalización de la ley de Ohm

$$ \widetilde{V} = \widetilde{I} Z ~~~~ (6) $$

donde $Z = Z_R+Z_L+Z_C$ es la impedancia total, formada por las impedancias:

$$ \begin{cases} \text{resistiva, } &Z_R =R ;\\ \text{inductiva, } &Z_L =i\omega L;\\ \text{capacitiva, } &Z_C =-\frac{i}{\omega c}. \end{cases} $$

En este contexto, a modo de repaso, el valor absoluto de la ley de Ohm (6) nos lleva a que

$$ I_0 = \frac{V_0}{|Z|} = \frac{V_0}{\sqrt{R^2+ \left( \omega L- \frac{1}{\omega C} \right)^2}}. ~~~~ (7) $$

Cuando la amplitud de la corriente es máxima, también lo es la amplitud de la potencia entregada al circuito (resonancia). Esto sucede cuando el denominador de la última expresión es mínimo. Lo cual sucede cuando la frecuencia adquiere un valor $\omega_R$ tal que la impedancia es puramente resistiva, es decir, cuando las impedancias inductiva y capacitiva se cancelan entre sí: $\omega_R L- \frac{1}{\omega_R C} = 0$. Así, la frecuencia de resonancia es

$$ \boxed{\omega_R^2= \frac{1}{LC}}. $$

d)

La potencia instantánea disipada por la bobina estará dada por $P(t)=I(t)V(t)$, es decir, teniendo en cuenta las relaciones (3) y (4)

$$ P(t) =I_0V_0 \cos (\omega t+\varphi’) \cos (\omega t+\varphi). $$

El producto de los cosenos puede expresarse como¹

$$ \cos (\omega t+\varphi’) \cos (\omega t+\varphi) = \frac{\cos (\varphi’-\varphi)+\cos (2\omega t+\varphi+\varphi’)}{2}. $$

entonces

$$ \boxed{P(t) = \frac{I_0 V_0\cos (\varphi’-\varphi)}{2} + \frac{I_0 V_0}{2} \cos (2\omega t+\varphi+\varphi’)} ~~~~ (8) $$

donde vemos que la potencia oscila alrededor del valor continuo $\frac{I_0V_0\cos (\varphi’-\varphi)}{2}$ con una amplitud igual a $I_0V_0/2$ a una frecuencia igual a $2\omega$.

Ya indiqué como se obtiene $I_0$. Para obtener la fase de la corriente, hay que recurrir a las definiciones (5) y a la ley de Ohm (6), para evidenciar que la impedancia

$$ Z = \frac{V_0}{I_0} e^{\varphi - \varphi’} $$

tiene un argumento igual a $\varphi - \varphi’$, de manera que la fase inicial de la corriente está determinada por la siguiente relación

$$ \tan (\varphi - \varphi’) = \frac{\omega L- \frac{1}{\omega C}}{R}. $$

En la resonancia, las fases iniciales entre la corriente y la tensión coinciden, de manera que tanto el valor continuo de la potencia como su amplitud de su oscilación son iguales a $\frac{I_0V_0}{2}$ y su fase inicial es el doble que la de la fuente.