N°04-2025

Enunciado

Un grafo $G$ es un conjunto de vértices ${v_1, \ldots, v_n}$ y enlaces que unen ciertos pares de vértices. Por ejemplo:

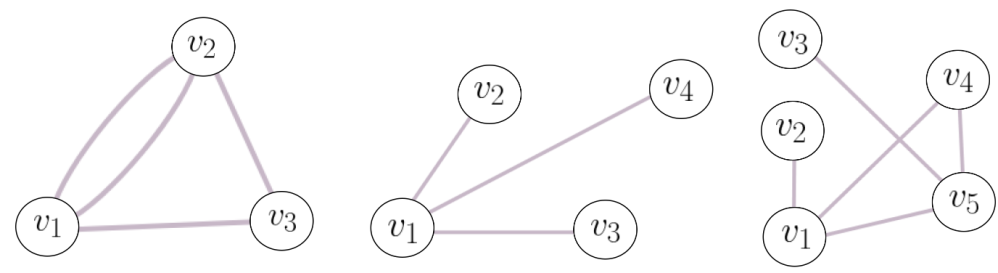
La matriz de adyacencia de un grafo $G$ con vértices $v_1, \ldots, v_n$ es la matriz cuadrada $A^G = (a_{ij})_{1 \leq i,j \leq n} \in \mathbb{R}^{n \times n}$ tal que $a_{ij}$ : cantidad de enlaces que unen $v_i$ con $v_j$. En los grafos de la figura de arriba, las matrices de adyacencia son:

$$ \begin{pmatrix} 0 & 2 & 1 \\ 2 & 0 & 1 \\ 1 & 1 & 0 \end{pmatrix}, \quad \begin{pmatrix} 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{pmatrix} \quad \text{y} \quad \begin{pmatrix} 0 & 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 & 0 \end{pmatrix} $$

a) Hallar la matriz de adyacencia del siguiente grafo.

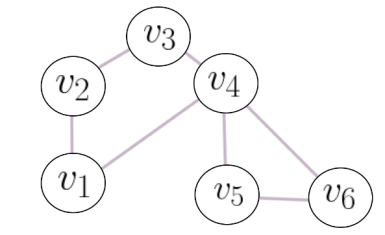
b) Un camino entre dos vértices $v_i$ y $v_j$ es la unión de ciertos enlaces del grafo, que nos permiten hacer un recorrido desde $v_i$ hasta $v_j$ (pasando, eventualmente, por algunos vértices intermedios). En el grafo $G$ del ítem (a), por ejemplo, los siguientes caminos unen $v_1$ con $v_6$ (aunque no son los únicos que lo hacen).

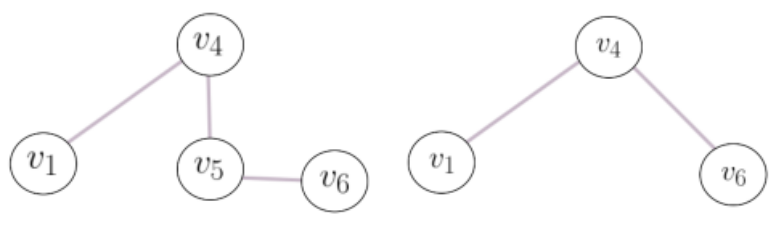
Dado un grafo $G$ con vértices ${v_1, \ldots, v_n}$, considerar la matriz:

$$ (b_{ij})_{1 \leq i,j \leq n} := A^G \cdot A^G $$

I) Probar que si $b_{lk} > 0$ entonces hay un camino que une $v_l$ con $v_k$.
II) Si hay un camino que une $v_l$ con $v_k$, ¿entonces $b_{lk} > 0$? Justificar.

c) Hallar un grafo de tres vértices de forma tal que su matriz de adyacencia no tenga como autovalor a $\lambda = 0$.

Resolución

a)

Basta con recurrir a la definición de matriz de adyacencia y escribir cuidadosamente

$$ \begin{pmatrix} 0 & 1 & 0 & 1 & 0 & 0\\ 1 & 0 & 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 1 & 0 & 0\\ 1 & 0 & 1 & 0 & 1 & 1\\ 0 & 0 & 0 & 1 & 0 & 1\\ 0 & 0 & 0 & 1 & 1 & 0 \end{pmatrix} $$

b)

I)

Como $(b_{ij})_{1 \leq i,j \leq n} := A^G \cdot A^G$ se trata de un producto matricial, podemos considerar el elemento $b_{lk}$ mediante la sumatoria
$$ b_{lk} = \sum_{i=1}^{n} a_{li} a_{ik}. $$

Si $b_{lk}>0$ entonces, debe existir al menos uno de los términos de la sumatoria que no sea nulo. Es decir, debe existir un valor de $i$ tal que $a_{li} a_{ik} $, lo cual es sólo posible si ambos factores son distintos de cero: $a_{li}\neq 0$ y $a_{ik}\neq 0$. Lo cual nos dice que existen caminos entre los vértices $v_l$ y $v_i$, como también entre $v_i$ y $v_k$. En cuyo caso existe un camino entre $v_l$ y $v_k$ a través de $v_i$: $$ v_l \leftrightarrow v_i \leftrightarrow v_k, $$ tal como queríamos demostrar.

II)

Podemos pensar en el grafo cuya matriz de adyacencia es

$$ A^{G} = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}, $$

donde estan conectados los vértices de una forma sencilla $v_1 \leftrightarrow v_2 \leftrightarrow v_3$. En este caso, $$ (b_{ij})_{1 \leq i,j \leq 3} := A^G \cdot A^G = \begin{pmatrix} 1 & 0 & 1 \\ 0 & 2 & 0 \\ 1 & 0 & 1 \end{pmatrix} $$

donde vemos que $b_{12}=0$ incluso a pesar de que hay un camino que une $v_1$ con $v_2$.

c)

Veremos dos formas de encontrar una matriz de adyacencia que no tenga a $0$ como autovalor. El enunciado tiene una tendencia a mostrar grafos cuyas matrices de adyacencia no tienen elementos en la diagonal. Sin embargo, no hay nada en su definición que impida que existan caminos que inicien y terminen en un mismo vértice (denominados bucles). Por ello, el grafo de tres vértices que tiene un bucle en cada vértice y ningún otro camino, tiene como matriz de adyacencia a la matriz identidad

$$ A^{G} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}, $$ que no tiene a $0$ como autovalor.

Si caemos en la trampa del enunciado y nos interesa buscar aquellas matrices (sin bucles) de la forma $$ A^{G} = \begin{pmatrix} 0 & a_1 & a_2 \\ a_1 & 0 & a_3 \\ a_2 & a_3 & 0 \end{pmatrix}, $$

que no tienen a cero como autovalor, podemos seguir la siguiente estrategia: buscar las condiciones necesarias para que tales matrices tengan ese autovalor (cero) y luego elegir cualquier matriz que no cumpla con ellas.

Si una matriz tiene a $0$ como autovalor, debe existir $\overline{u} \neq \overline{0}$ tal que $A^G \bar{u} = \overline{0}$. Lo cual es posible sólo si la matriz $A^G$ no tiene inversa.

Así, todas aquellas matrices que sí tengan inversa, no tendran a cero como autovalor. En ese caso, se debe cumplir que $\det \left( A^G \right) \neq 0$. Como

$$ \det \left( A^G \right) = a_1 a_2 a_3 + a_2 a_1 a_3 = 2 a_1 a_2 a_3, $$ entonces buscamos aquellas matrices tales que $a_1 \neq 0$, $a_2 \neq 0$ y $a_3 \neq 0$. Por ejemplo, el triángulo dado por la matriz de adyacencia

$$ A^{G} = \begin{pmatrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{pmatrix}. $$