N°18-2024

Enunciado

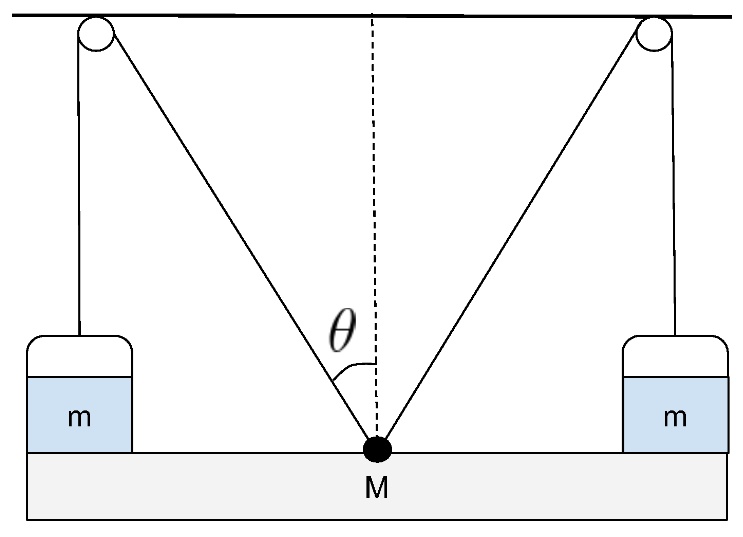
Dos baldes de masa despreciable, ambos inicialmente llenos con la misma cantidad de agua de masa $m$, y una tabla homogénea de masa $M$ cuelgan de sogas inextensibles. Las sogas pasan por dos poleas fijas al techo y están atadas al punto medio de la tabla. Todo el sistema está inicialmente en equilibrio y los baldes hacen contacto con la tabla, tal como se muestra en la figura.

a) Si los baldes pierden agua al mismo ritmo y $m$ disminuye lentamente en el tiempo, ¿para qué masa $m$ dejan de hacer contacto con la tabla?
b) Describir cualitativamente lo que sucede luego que los baldes dejan de hacer contacto con la tabla.

Resolución

Comencemos estudiando las interacciones (Figura A). La tabla interactúa con la tierra a través de su peso $Mg$ y a través de dos mecanismos de interacción con cada uno de los baldes: de contacto a través de la fuerza normla $N$ y usando como vehículo de interacción a la cuerda que generan fuerzas de tensión $T$. Por lo anterior, ya vemos que las fuerzas de interacción entre un balde y la tabla tendrán sus correspondientes reacciones, a las cuales se suma su peso $mg$.

En este contexto, los balances de fuerzas sobre la tabla y uno de los baldes (la situación es la misma en el otro) están dados por:

$$ \begin{cases} \begin{split} \sum F_{balde} &= T+N-mg \\ \sum F_{tabla} &= 2T \cos \theta -2N-Mg \end{split} \end{cases} ~~~~~~~ (1) $$

a)

Para determinar a partir de qué valor de $m$ los blades se desprenden de la tabla, podemos determinar la condición que debe cumplir $m$ para que el sistema permanezca en contacto y obtener los valores de $m$ para los cuales se produce el desprendimiento como el complemento de la condición obtenida. Esta es una estrategia prolija y cómoda desde un punto de vista estratégico, ya que mientras las partes del sistemas están en contacto mutuo se encuentran en equilibrio y podemos igualar cada uno de los balances de (1) a cero:

$$ \begin{cases} \begin{split} 0 &= T+N-mg\\ 0 &= 2T \cos \theta -2N-Mg \end{split} \end{cases} $$

Lo que debemos hacer es imponer que el contacto se mantiene, lo cuál se expresa matemáticamente pidiendo que $N>0$. Pero antes nos independicemos de $T$:

$$ \begin{split} 0 &=2(mg-N) \cos \theta -2N-Mg \\ 0 &=2mg\cos \theta -2N(1+\cos \theta)-Mg\\ 2mg\cos \theta &= 2N(1+\cos \theta)+Mg. \end{split} $$

Y ahora si, pedir que $N>0$ implica pedir $2N(1+\cos \theta)>0$ y por lo tanto que $2mg\cos \theta >Mg$, que nos permite decir que:

$$ \boxed{\text{Si } m>\frac{M}{2 \cos \theta} \Rightarrow \text{El sistema permanece en contacto}} $$

Así, podemos decir que

$$ \boxed{\text{A partir del valor crítico } m_c=\frac{M}{2 \cos \theta} \text{ los baldes se desprenden.}} $$

Estoy aprovechando esta oportunidad para mostrarte un procedimiento que suele ayudar mucho en los problemas de desprendimiento. Estudiar las condiciones de contacto nos permite manipular ecuaciones y desigualdades con prolijidad conceptual y matemática. Obtenemos las condiciones de contacto para luego obtener los parámetros críticos y las condiciones de desprendimiento como su complemento.

Éste método no es generalizable, a veces sucederá que es otra la estrategia más adecuada. Así como a veces no tenes porque realizar tu aporte libre y voluntario. ¡O quizá si! Gracias, sin importar lo anterior, por llegar hasta aquí. Sigamos.

b)

Cuando los baldes se desprendan, el ángulo que subtiende la cuerda con la vertical cambiará. Le podemos llamar genéricamente $\phi$. También sucederá que $N=0$, entonces los balances de fuerzas dados por las relaciones (1) producirán aceleraciones que deben cumplir las siguientes relaciones:

$$ \begin{cases} \begin{split} T-mg &= m a_m\\ 2T \cos \phi -Mg &= M a_M. \end{split} \end{cases} $$

En un intento por entender qué sucede podemos nuevamente independizarnos de la tensión $T$ y reorganizar para obtener la siguiente expresión:

$$ M a_M = 2m a_m \cos \phi + [ 2m \cos \phi -M] g. ~~~~~~~ (2) $$

Por como elegimos el sistema de coordenadas (positivo hacia arriba y negativo hacia abajo), la tabla aumentará su velocidad de caída mientras $a_M<0$. En ese caso $a_m>0$, ya que la cuerda es inextensible y cuando la tabla se acelera en una dirección los baldes lo hacen en la dirección contraria. Para que todas esas condiciones puedan cumplirse es indispensable, aunque no suficiente, que el segundo termino del segundo miembro sea negativo. Es decir, se debe cumplir que

$$ m \cos \phi < \frac{M}{2}. $$

Para entender mejor esta condición podemos hacer uso del valor crítico $m_c$ obtenido en el inciso anterior, de manera que la condición es equivalente a:

$$ \frac{m}{m_c} \frac{\cos \phi}{\cos \theta} < 1. ~~~~~~~ (3) $$

Se observa una competencia entre los dos cocientes. Por un lado $\frac{m}{m_c}<1$ y disminuye con el tiempo. Por el otro, como $\phi<\theta$ entonces $\cos \phi> \cos \theta$, lo cual es equivalente a decir que $\frac{\cos \phi}{\cos \theta} > 1$. Además, este cociente aumenta con el tiempo . Así, se nos manifiestan las siguientes posibilidades:

• $m$ disminuye a un ritmo tal que siempre se cumple la condición (3), es decir, la tabla se acelera en caída;

• a medida que la tabla cae, el ángulo $\phi$ podría disminuir hasta un valor que impida el cumplimiento de la condición (3), que es necesaria para que la tabla se acelere en caída. Esto produciría una inversión aceleraciones, hasta que posiblemente, por la inevitable disminución de $m$ se produciría una nueva inversión. En este contexto, la inversión de las aceleraciones podría producirse sucesivas veces ad infinitum. Incluso, la situación nos invita a preguntarnos ¿será posible un movimiento oscilatorio?. La complejidad de este asunto está supeditada a la forma en que la masa de los baldes $m$ disminuya respecto de la disminución de $\phi$. Podríamos avanzar en el análisis, pero no nos piden tanto.

A través de alguno de los procesos transitorios descritos, el sistema podría llegar a un estado estacionario de velocidades contantes. En ese caso, es fácil deducir a partir de (2) que el sistema entrará en tal estado en el instante en que la masa de los baldes y el ángulo cumplan con la condición $2m_e \cos \phi_e =M$ o su equivalente

$$ \frac{m_e}{m_c} \frac{\cos \phi_e}{\cos \theta} = 1. $$

$$ \boxed{\text{FIN}} $$