N°17-2024

Enunciado

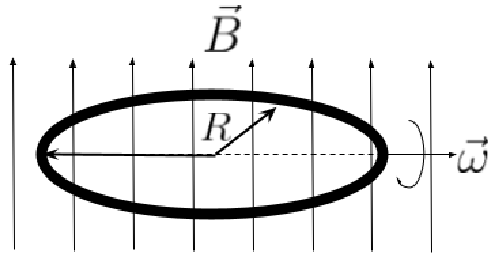
Una espira circular de cobre de radio $R$ gira a una velocidad angular $\omega$ constante alrededor de un eje diametral en un campo magnético $\bar{B}$ constante y uniforme, perpendicular al eje de rotación, como se muestra en la figura. El sistema se encuentra en un estado estacionario.

a) Graficar esquemáticamente la corriente en la espira en función del tiempo.
b) ¿Se espera que la espira de cobre esté a una temperatura mayor, menor o igual a la temperatura del ambiente? Justificar.

Resolución

a)

La rotación de la espira produce una variación de flujo magnético $\Phi = \int_{S} \bar{B} \cdot d \bar{S}$. Entonces, por la ley de Faraday-Lenz sabemos que se generará una fuerza electromotriz $\mathcal{E} = - \frac{d \Phi}{d t}$ que pondrá en circulación las cargas, es decir, producirá una corriente $I$.

Vamos paso a paso. El flujo estará determinado por la orientación del eje de la espira respecto del campo magnético $\bar{B}$. Como la dirección del eje está dado por el vector superficie $d \bar{S}$, si él angulo que subtiende con $\bar{B}$ es $\theta = \omega t$ (estamos eligiendo el origen temporal cuando los vectores coinciden en dirección):

$$ \begin{split} \Phi &= \int_{S} \bar{B} \cdot d \bar{S} \\ &= \int_{S} BdS \cos \theta \\ &= B \cos \theta \int_{S} dS \\ &= B \cos\theta S \\ \Phi &= BS \cos (\omega t). \end{split} $$

Así, la f.e.m producida está dada por

$$ \mathcal{E} = - \frac{d \Phi}{d t} = BS\omega \sin (\omega t) ~~~~~~ (1). $$

Finalmente, por la ley de Ohm, tendremos que la corriente está dada por $I =\frac{\mathcal{E}}{r}$, donde $r$ es la resistencia de la espira. Entonces,

$$ \boxed{ I= \frac{BS\omega}{r} \sin (\omega t)}, $$

es decir, se trata de una corriente alterna cuya frecuencia es $\omega$. Rápidamente vemos que mientras la magnitud e campo magnético y la superficie que define la espira determinan proporcionalmente la amplitud la resitencia la define a través de una proporcionalidad inversa. También es importante notar que la velocidad angular $\omega$ no solo deifne la periodicidad sino ta bién su ampitud, de manera que sucede que a mayores frecuencias mayores amplitudes. A continuación tenemos un esquema del comportamiento temporal de la corriente, donde podemos variar los parámetros intervinientes a gusto.

b)

Una magnitud característica de una espira es su momento magnético $\bar{M}=I \bar{S}$, el cuál está dado por la corriente que $I$ circula por ella, la superficie $S$ de la espira y tiene la misma dirección de su eje, por ello, el vector $\bar{S}$ tiene magnitud $S$ y apunta en al dirección del eje.

Una espira con momento magnético en presencia de un campo magnético $\bar{B}$ exerimenta un torque dado por $\overline{\tau} = \bar{M} \times \bar{B}$. Así, para que el sistema se mantenga en un estado estacionario, será necesario realizar un torque en el eje que compense el torque debido a la interacción entre la espira y el campo magnético. También podemos realizar un análisis energético y pensar que será necesario realizar un trabajo rotacional elementa dado por $d W = \tau d \theta$, que implicará la entrega de una potencia que podemos desarrollar de la siguiente forma

$$ \begin{split} P &= \frac{d W}{d t} \\ &= \tau \frac{d W\theta}{d t} \\ &= \tau \frac{d \theta}{d t} \\ &= \tau \omega \end{split} $$

como $\tau = M B \cos (\theta)$

$$ \begin{split} P &= M B \omega \cos (\theta) \\ &= I S B \omega \cos (\omega t) \\ &= I [S B \omega \cos (\omega t)] \end{split} $$

donde podemos identificar la f.e.m. dada por al relación (1) y por lo tanto

$$ P = I \mathcal{E}. $$

Es decir, la potencia mecánica que se realiza sobre el sistema para mantenerlo en un estado estacionario se traduce en potencia eléctrica, que a su vez se disipa por efecto Joule. Esa disipación necesariamente debe involucrar el aumento de temperatura de la espira para comenzar a intercambiar calor con el ambiente.

Este fenómeno no es otra cosa que un generador de corriente alterna.

Dame una manito para tener tiempo de hacer más publicaciones con tu aporte libre y voluntario.