N°09-2024

Enunciado

Se exploró un sistema de túneles y cuevas subterráneos que se encuentran parcialmente inundados y que tiene atrapado aire en dos zonas de su interior (llamadas cámaras de aire). El mismo posee una sola entrada, y ninguna salida. Este sistema se puede aproximar como una sucesión de cilindros horizontales y verticales conectados, como se muestra en la figura. Los túneles poseen un diámetro aproximado de $1 m$, y las cuevas uno de $10 m$. En la figura se muestran además las cotas donde se encontraron los niveles de agua (las interfaces aire/agua), tomando como referencia la cota de la entrada. Estimar la presión en $B$, sabiendo que $A$ está a $1~\text{atm}$ y que la densidad del agua es de aproximadamente $1000~\text{kg/m}^3$. Despreciar la densidad del aire y la tensión superficial en todas las interfaces aire/agua.

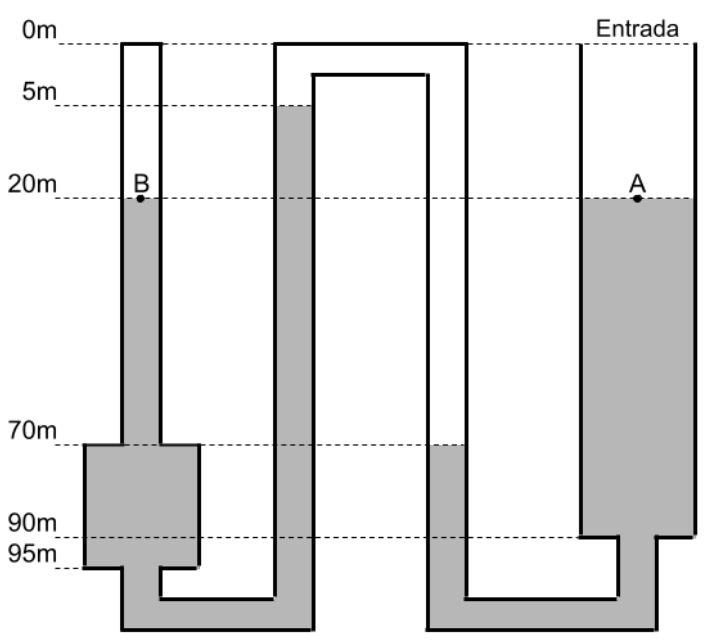
Resolución

Para resolver el problema de la forma más simple posible, tendremos en cuenta (Figura A) que las presiones en los punto $B$ y $B’$ son las mismas, como también lo son las presiones en los puntos $C$, $C’$ y $C’’$ . Así, tendremos las siguientes igualdades

$$ \begin{split} P_{B}&= P_{B’} = P_{C’’}+\rho g H_{C’’ B’} \\ P_{C’’}&= P_{C’} = P_{C}= P_{A}+\rho g H_{AC} \end{split} $$

que mezclándolas nos permiten obtener que

$$ P_{B} = P_{A}+\rho g \left( H_{C’’ B’} + H_{AC} \right). $$

Como $H_{C’’ B’} + H_{AC}=H_{C’C’’}=65~\text{m}$, $\rho = 1000~\text{kg/m}^3$ y $g=9.8~\text{m/s}^2$ y $P_A= 1~\text{atm} \approx 101325~\text{Pa}$:

$$ \begin{split} P_{B} &\approx 101325~\text{Pa}+\left(1000~\text{kg/m}^3 \right) \left( 9.8~\text{m/s}^2 \right) \left( 65~\text{m} \right)\\ P_{B} &\approx 101325~\text{Pa}+637000~\text{Pa}\\ \end{split} $$ es decir, $\boxed{P_B\approx 738325~\text{Pa}\approx 7.29~\text{atm}}$. ¡Siete veces la presión atmosférica a la misma altura! Que increíble.

Si todavía no lo hiciste y valoras el trabajo, siempre estas a tiempo de hacer tu aporte libre y voluntario. ¡Gracias!