N°08-2024

Enunciado

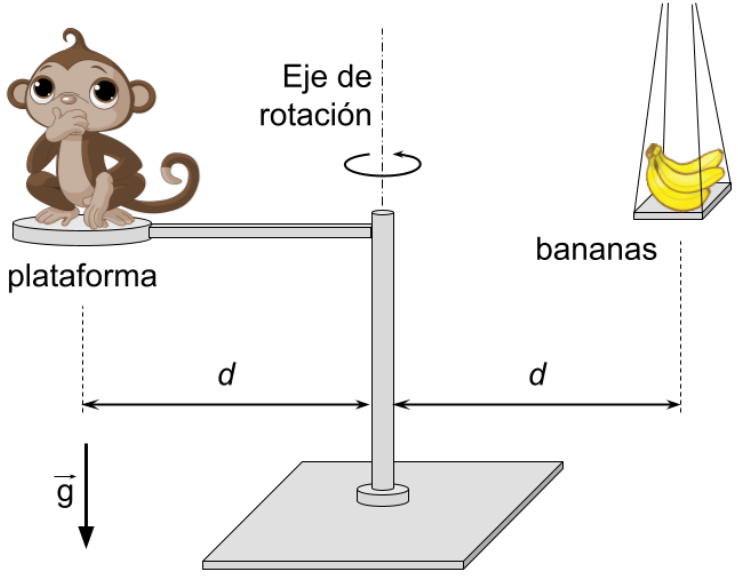
Un monito se encuentra sobre una plataforma, la cual puede girar libremente y sin rozamiento en el plano horizontal, alrededor de un eje vertical. Del lado opuesto a la plataforma hay bananas, que el monito hambriento desea alcanzar. El monito no puede abandonar su plataforma, la cual está inicialmente en reposo.

¿Hay algún movimiento posible del monito sobre la plataforma que le permita alcanzar las bananas? Justificar la respuesta.

Resolución

Me tomé el trabajo de recopilar comentarios durante el mismo día del examen. Algunas también son reacciones de personas que no rindieron pero mantienen un vivo interés en el proceso de selección. Me parece que es un punto de partida interesante:

Reacciones y comentarios populares

Lo único que se me ocurre la mutilación.

Yo puse que no, no podia el mono porque no se daba la conservación del momento, ademas no tiene impulso el mono… necesitaba un jet pack.

Podría soplar si hay resistencia del aire … (minutos después) ahora que lo pienso, el mono respira expandiendo y comprimiendo el diafragma, y ese se expande/contrae radialmente simétrico, asi que no generaría una fuerza contraria super fuerte al viento del soplo, asi que…

Yo puse algo como “Solo puede hacer fuerzas internas, así que no puede hacer cosas que lo giren”. Luego “Si tuviera un zapato o una piedra, podría tirarla y por conservación de momento llegar”. Y luego dibuje un mono tirando una piedra. Pero esto con énfasis de que el mono solito, solito, no podía.

Yo puse que el mono extendía el brazo (en un movimiento rotacional) mas externo con respecto al eje de giro y que lo dejaba extendido entonces si generaba momento y eventualmente llegaba a sus bananas.

Si el monito gira sobre si mismo, al no haber fuerza externa debe conservarse el momento angular=0 entonces la plataforma comienza a girar ¿?.

Si gira la cola con el eje de rotación paralelo a la barra hace precesión giroscópica.

Puse que escupía. Iba a llegar deshidratado para comer las bananas, pero bueno.

Yo puse que si el mono saltaba con una precisión exacta, al saltar haría girar la plataforma y mientras está en el aire, la plataforma llegaría hasta el punto dónde aterriza el mono.

Vieron las personas que hacen gimnasia competitiva que se balancean en una barra y dan vueltas?

Yo puse que en caso de que considere la resistencia del aire, con cualquier movimiento del mono puede causar un movimiento en la plataforma. Y si no se considera la resistencia del aire no podría moverse.

Inhalando para arriba y soplando hacia adelante puede llegar. (Otra persona responde: “inhalando de costado también”; y luego otra: “inhalando para adelante y soplando para atrás también”)

El mono tiene que hacer como Colitas.

Yo lo pensé de esa forma también, si el mono se parara de manos, se dejara caer hacia el lado de sus palmas, absorbiendo la fuerza reactiva de la plataforma con el abdomen, le aplicaría una fuerza a la plataforma que lo acelera.

Me hace acordar al capítulo de los Simpson.

Ballora de fnaf sister location se movía de asi a traves de la unión de sus pies en punta girando sobre su eje.

El mono bailarín es la mejor solución.

Mejor solución

Definitivamente, coincido con el último comentario, el mono bailarín es la mejor solución. Aquí, como lo dice alguno de los comentarios, el principio que nos permite analizar la situación es la conservación del momento angular. Podemos recurrir a su conservación ya que el momento (o torque) sumario de todas las fuerzas externas es nulo. Esto se debe, principalmente, a que el eje se encarga de balancear los momentos producidos por el peso del mono y el de la plataforma misma. A su vez, el eje no aporta momento por rozamiento. Así, el momento angular total, constituido por el momento angular del mono $\bar{L}_{M}$ y el de la plataforma $\bar{L}_P$, debe mantenerse nulo al igual que al principio:

$$ \bar{L}_{M} + \bar{L}_P = \bar{0} ~~~~~~~~ (1) $$

Si $I_P$ es el momento de inercia de la plataforma respecto de su propio eje $\bar{\Omega}$ a la velocidad angular de la plataforma, podemos expresar su momento angular coo $$ \bar{L}_P = I_P \bar{\Omega} $$

El momento angular del mono estará compuesto por dos contribuciones, una debida a la traslación del centro de masas y la otra debida a la rotación del mono respecto del centro de masas:

$$ \bar{L}_M = \overline{r} \times \overline{p}_M + \bar{L}_{M-CM} $$

Denominemos $I_M$ al momento de inercia del mono respecto de su centro de masas y $\bar{\omega}$ a su velocidad angular, entonces $\bar{L}_{M-CM} = I_M \bar{\omega}$. A su vez, como $\overline{r} \times \overline{p}_M = m \overline{r} \times \overline{v}_M = m d v_M \hat{\Omega}$, y la velocidad del centro de masas del mono es $v_M= \Omega d$:

$$ \bar{L}_M = m d^2 \bar{\Omega} + I_M \bar{\omega} $$

Si aprovechamos la conservación expresada en (1), junto a (2) y (3) podemos obtener la velocidad de la plataforma en término del resto de los parámetros:

$$ \bar{\Omega} =-\frac{I_M}{I_P+m d^2}\bar{\omega}. $$

donde vemos que el mono impedido de engordar para aumentar su masa y condicionado para aumentar la distancia $d$, puede aumentar su momento de inercia extendiendo los brazos y girar a la mayor velocidad angular a la cual esté acostumbrado, para maximizar la velocidad angular de la plataforma, que girará en sentido contrario.

Todo esto sería posible si el mono supiera de la conservación del momento angular, pero como no existen arboles de este estilo que le hayan permitido aprenderlo desde un punto de vista evolutivo: la tiene difícil.

¿Por qué es la mejor solución?

Principalmente porque este método podría llevarse adelante sin dificultad, más allá de la idealización del problema,. Incluso si la plataforma tuviese algo de rozamiento y hubiera resistencia con el aire, con suficiente prolijidad acrobática, el mono podría vencer sus efectos girando a mayor velocidad y aumentando su momento de inercia.

Los efectos producidos por este tipo de fenómenos pueden sorprenderte. Si alguna vez los experimentaste, sabes de qué estoy hablando. Y sino, proba sentándote en una silla giratoria con unas pesa en cada mano y los brazos extendidos (para aumentar tu momento de inercia), luego pedile a alguien que te haga girar y unos instantes después, cerra tus brazos.

Después de girar por un buen rato, podes tomar el siguiente antídoto para que se pase el mareo: le llamamos aporte libre y voluntario. ¡Gracias!