N°05-2024

Enunciado

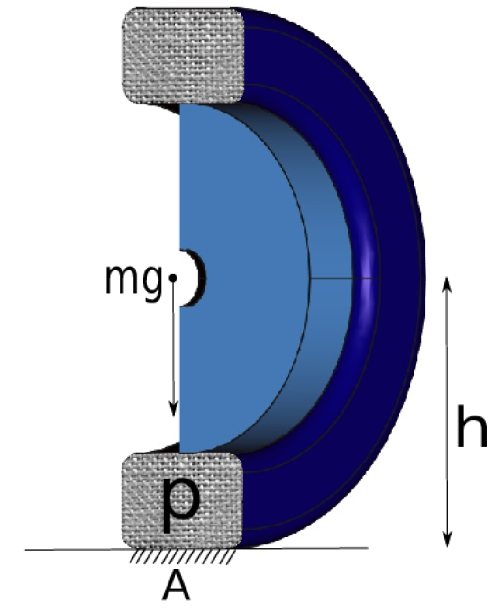
Se tiene un neumático como el que se ilustra en la figura. El neumático tiene una masa $m$, de manera tal que, en equilibrio, su peso $mg$ deforma la base y genera una superficie de contacto con el piso de área $A_0$ . En esas condiciones la altura desde el piso al eje de la rueda es $h_0$ , y la presión del aire en el interior de la misma es $p_0$.

a) Encontrar la relación entre $m$, $A_0$ , $p_0$ y $h_0$ , para la condición de equilibrio estático.

A tiempo $t = 0$ se perturba el equilibrio del sistema de manera que $h$ varía con el tiempo:

$$ h(t)= h_0 - z(t). $$

Por las características constructivas de la rueda se sabe que ante esta variación de $h$ se cumplen las siguientes relaciones:

$$ p(t)= p_0 + k_p z(t) ~~~~~ \text{y} ~~~~ A(t)= A_0 + k_A z(t) $$

donde $k_A$ y $k_p$ son constantes y no negativas.

b) Escribir la ecuación de movimiento del sistema perturbado.

c) Escribir las condiciones para que el sistema se comporte como un oscilador armónico.

Despreciar la rigidez del neumático.

Resolución

Para todo lo sucesivo, es inevitable que realicemos un análisis de la superposición de interacciones en el neumático (Figura A). En todo el análisis nos olvidaremos de las fuerzas atmosféricas que se ejercen desde el centro del neumático y las que se ejercen lateralmente (en la dirección perpendicular al dibujo de la Figura A), ya que en todo momento se cancelan entre sí por simetría. Además del peso $mg$ tendremos la fuerza de contacto con del suelo, $N$. La deformación conlleva una asimetría en el efecto atmosférico sobre el neumático, de manera que sobre la superficie superior cuya proyección es $A$ (color verde) la fuerza tiene un magnitud igual a $P_{atm}A$ mientras que en el resto de la superficie en contacto con la atmósfera las interacciones se balancean (color dorado). Así la superposición de fuerzas estará dada por

$$ \sum_i F_i = N-P_{atm}A-mg ~~~~~~ (1) $$

Para determinar la fuerza de contacto $N$ podemos realizar un análisis de las interacciones sólo en la parte del neumático que se encuentra en contacto con el suelo y, por lo tanto, en equilibro. Como muestra la Figura B, sobre este sector del neumático actúa su peso $m_cg$ y la fuerza de presión interna $pA$ que como a su vez son balanceadas por la fuerza de contacto $N$:

$$ N=m_cg+pA. $$

Remplazando en la relación (1) tenemos que

$$ \sum_i F_i = (p-P_{atm})A-(m-m_c)g. ~~~~~~ (2) $$

De aquí en más, la complejidad del problema está supeditada a la relación entre la masa total del neumático $m$ y la parte de su masa que está en contacto $m_c$. En general no es sólo el peso del neumático lo que produce la deformación del mismo sino el peso del vehículo distribuido en todos sus neumáticos. En ese caso $$m_c \ll m$$ y la relación (2) se simplifica:

$$ \sum F = (p-P_{atm})A-mg. ~~~~~~ (3) $$

Avanzaremos en el planteo bajo esta última hipótesis.

a)

En el equilibrio el área de contacto con el suelo es $A_0$ y la presión $p_0$, de manera que $$ (p_0-P_{atm})A_0=mg ~~~~~~ (4) $$

La presencia de la altura al eje $h_0$ se dá de manera implícita en el área $A_0$, que si el ancho del neumático es $e$ y su radio $R$, entonces

$$ R^2 = h_0^2 + \left( \frac{A_0}{2e} \right)^2, $$

relación que es válida para cualquier altura $h$ y área $A$. Es fácil de deducir teniendo en cuenta el esquema de la Figura C.

b)

Para el sistema perturbado, teniendo en cuenta la ecuación (3), la ecuación de movimiento es de la forma $$ (p-P_{atm})A-mg = m \frac{d^2 h_{CM}}{d t^2} $$

Como $m_c \ll m$, entonces $h_{CM} \approx h = h_0-z$ y podemos desarrollar la ecuación de movimiento de la siguiente manera:

$$ \begin{split} (p-P_{atm})A-mg =& - m \ddot{z} \\ (p_0+k_pz-P_{atm})(A_0+k_Az)-mg =& - m \ddot{z} \\ (p_0-P_{atm})(A_0+k_Az)+k_pz(A_0+k_Az)-mg =& - m \ddot{z} \\ (p_0-P_{atm})A_0 +(p_0-P_{atm})k_Az+k_pz(A_0+k_Az)-mg =& - m \ddot{z}. \end{split} $$

Teniendo en cuenta la relación (4), $(p_0-P_{atm})A_0=mg$, entonces

$$ \begin{split} \frac{mg}{A_0}k_Az+k_pz(A_0+k_Az)=& - m \ddot{z} \\ \left[ \frac{mg}{A_0}k_A+k_pA_0\right] z + k_p k_Az^2=& - m \ddot{z}, \end{split} $$ es decir,

$$ \boxed{m\ddot{z} + \left[ \frac{mgk_A}{A_0}+k_pA_0\right] z + k_p k_Az^2= 0 }. $$

c)

Para que la oscilación sea armónica debería suceder que el término cuadrático en $z$ sea despreciable respecto del término lineal:

$$ \begin{split} \left[ \frac{mgk_A}{A_0}+k_pA_0\right] z &\gg k_p k_Az^2 \\ \left[ \frac{mgk_A}{A_0}+k_pA_0\right] &\gg k_p k_Az. \end{split} $$

Lo que nos lleva a que

$$ \boxed{z \ll \left[ \frac{mg}{A_0k_p}+\frac{A_0}{k_A}\right]}. $$

Aproximación auspiciada por el aporte libre y voluntario. ¡Gracias!