N°03-2024

Enunciado

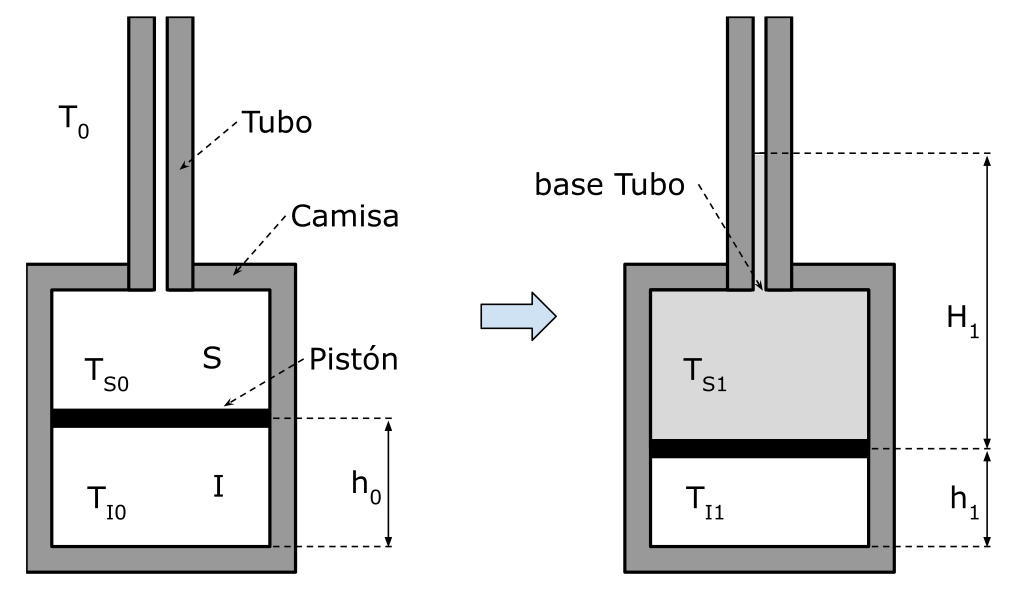
Sea un pistón de masa $M$ y espesor despreciable, el cual se puede desplazar libremente en la dirección vertical, dentro de una camisa adiabática, la cual tiene una base de área $A_c = 50 ~ \text{cm}^2$ y una altura $L = 1 ~ \text{m}$. El pistón divide a la camisa en dos cámaras, una estanca inferior $I$ llena de un gas ideal monoatómico, y una superior $S$ conectada a la atmósfera mediante un tubo de área interna $A_t = 1 ~ \text{cm}^2$.

a) Inicialmente, todo el sistema se encuentra en equilibrio con la atmósfera, la cual está a una temperatura $T_0 = 5^{\circ}\text{C}$ y una presión $P_0 = 10^5 ~ \text{Pa}$. En estas condiciones, la cámara inferior posee una altura $h_0 = L/2$ y una presión $P_{I_0} = 1,1 \cdot 10^5 ~ \text{Pa}$. Determinar la masa $M$ del pistón.

b) Luego, instantáneamente se llena la cámara superior y parte del tubo (hasta una altura $H_1$ respecto del pistón) con agua caliente a $T_{S_1} = 95^{\circ}\text{C}$, hasta que la presión del gas dentro de la cámara inferior llega a $P_{I_1} = 1,2 · 10^5 ~ \text{Pa}$. Determinar la masa de agua agregada, suponiendo que no hay intercambio de calor entre ambas cámaras, que la densidad del agua es de $\rho = 1 ~ \text{kg/dm}^3$ , y la gravedad posee un valor de $g = 9,8 ~ \text{m/s}^2$ . Calcular además la nueva altura $h_1$ que posee la cámara inferior.

c) Luego del llenado rápido, se cierra una válvula que está en la base del tubo, y que aı́sla a éste de la cámara superior. Finalmente se espera el tiempo suficiente para que se equilibren las temperaturas del gas en la cámara inferior con la del agua en la cámara superior. Determinar la presión $P_{I_2}$ dentro de la cámara inferior y su nueva temperatura, para cuando se alcance el equilibrio térmico mencionado, suponiendo que no hay intercambio de calor con la atmósfera, despreciando la inercia térmica de las paredes del pistón y la camisa, y despreciando también el coeficiente de dilatación del agua. Considerar que el agua es incompresible y posee un calor especı́fico $C = 4,2 ~ \text{J/(gK)}$.

Resolución

a)

Inicialmente las fuerzas que actúan sobre el pistón (Figura A) son el peso $Mg$, la fuerza de presión $P_0A_c$ ejercida por la atmósfera en la cámara superior y la fuerza de presión $P_{I_0}A_c$ ejercida por el gas de la cámara inferior. Así, para que suceda el equilibrio debe cumplirse que

$$ P_{I_0}A_c - P_0A_c -Mg =0, $$

de donde resulta que

$$ \boxed{M=\frac{(P_{I_0}-P_0)A_c}{g}} $$

y cuyo valor es $\boxed{M \approx 5.1 ~ \text{kg}}$.

b)

Muchas veces, aunque no siempre, para averiguar el valor de una magnitud física es necesario partir de su expresión primaria e ir buscando la forma de desarrollarla hasta lograr que quede expresada en términos de los parámetros que conocemos. En este caso, la masa de agua que se vierte por el tubo (Figura B) estará dada por el producto de su densidad y su volumen:

$$ M_a= \rho V_a. $$

A su vez, una parte $A_c H_c$ del líquido se encuentra en la cámara superior y otra $A_t H_t$ en el tubo, por lo que podemos escribir la masa como

$$ M_a= \rho \left( A_c H_c + A_t H_t\right). $$

Como $H_1=H_c+H_t$, entonces

$$ M_a= \rho \left[ (A_c-A_t) H_c + A_t H_1\right]. ~~~~~~~ (1) $$

Vemos hasta aquí, que hemos convertido el problema de la determinación de la masa de agua $M_a$ en la determinación de las alturas $H_c$ y $H_1$, ya que es lo único que no conocemos en la relación (1).

Variación de la presión

La variación de la presión en el gas se debe sólo a la presión producida por la columna de agua, de manera que

$$ P_{I_1}-P_{I_0} = \rho g H_1, $$ entonces

$$ H_1 = \frac{(P_{I_1}-P_{I_0} )}{\rho g}. ~~~~~~~~~~(2) $$

Variables (ecuación) de estado del gas

Como la variación de la presión del gas se produjo sin intercambio de calor con los sistemas que le son externos, el proceso es adiabático. Además no hay variación en la cantidad de materia, por lo tanto

$$ P_{I_1} V_1^{\gamma} = P_{I_0} V_0^{\gamma}, $$

donde $V_1$ y $V_0$ son los volúmenes final e inicial, respectivamente, y el coeficiente de dilatación adibática $\gamma=5/3$ para un gas monoatómico. Como ambos volúmenes son proporcionales al área de la cámara, la misma relación vale para las alturas del gas

$$ P_{I_1} h_1^{\gamma} = P_{I_0} h_0^{\gamma}, $$

por lo que teniendo en cuenta que $h_0=L/2$ nos permite obtener la altura final del gas:

$$ \boxed{h_1 = \left( \frac{P_{I_0}}{P_{I_1}} \right)^{\frac{1}{\gamma}} \frac{L}{2}} ~~~~~~~~~(3) $$ cuyo valor es $\boxed{h_1 \approx 0.47 ~ \text{m}}$

Luego, dado que $L=h_1+H_c$ tendremos que

$$ H_c = \left(1 - \frac{1}{2} \left( \frac{P_{I_0}}{P_{I_1}} \right)^{\frac{1}{\gamma}} \right) L ~~~~~~~~~(4) $$

Determinación de la masa de agua

Si remplazamos las relaciones (2) y (4) en (1) tenemos que $$ \boxed{M_a= \rho \left[ (A_c-A_t) \left(1 - \frac{1}{2} \left( \frac{P_{I_0}}{P_{I_1}} \right)^{\frac{1}{\gamma}} \right) L + A_t \frac{(P_{I_1}-P_{I_0} )}{\rho g}\right]}. $$

cuyo valor es $\boxed{M_a \approx 2.67 ~ \text{kg}}$.

Intente simplificar al máximo la claridad en el procedimiento, decime si ese esfuerzo no merece un aporte libre y voluntario. ¡Gracias!. Para lo que sigue hice el mismo esfuerzo.

c)

Primero determinemos la masa de agua que queda en la cámara luego de cerrar la válvula. Para ello aprovechemos que la densidad del agua púede expresarse como

$$ \rho = \frac{M_c}{V_c} = \frac{M_c}{A_c H_c}, $$

es decir, despejando y remplazando la relación (4):

$$ M_c = \rho A_c \left(1 - \frac{1}{2} \left( \frac{P_{I_0}}{P_{I_1}} \right)^{\frac{1}{\gamma}} \right) L \approx 2.63 ~ \text{kg}. $$

Cómo consideraremos al agua incompresible, el volumen del gas no cambiará y en el proceso no habrá trabajo. Por ello, por el Primer Principio de la Termodinámica, el calor $Q$ transferido del agua al gas debe balancearse con la variación de su energía interna $\Delta U$:

$$ Q+\Delta U= 0 $$

Si $T$ es la temperatura final del sistema, el calor entregado por el agua estará dado por

$$ Q=M_c C (T-T_{S_1}), $$

mientras que si $n$ es la cantidad de moles del gas y $c_v$ su calor específico a volumen constante:

$$ \Delta U= n c_V (T-T_1) $$

entonces

$$ \begin{split} M_c C (T-T_{S_1})+n c_V (T-T_1)&=0 \\ (M_c C+n c_V) T- M_c C T_{S_1} - n c_V T_1 &=0 \\ \end{split} $$

entonces $$ \boxed{T=\frac{M_c CT_{S_1}+n c_VT_1}{M_c C+n c_V}}. ~~~~~~~~(5) $$

Como el calor específico a volumen constante de un gas monoatómico está dado por $c_V=\frac{3}{2}R$ sólo nos falta determinar el número de moles del gas y la temperatura $T_1$ a la que el gas quedó luego del proceso adiabático. Para ello escribiremos la ecuación de estado del gas inicialmente y desarrollaremos:

$$ \begin{split} P_{I_0} V_0&= n R T_0 \\ P_{I_0} A_c h_0&= n R T_0 \\ P_{I_0} A_c \frac{L}{2}&= n R T_0 \\ n R&=\frac{P_{I_0} A_cL}{2T_0} \\ n\frac{3}{2}R&=\frac{3P_{I_0} A_cL}{4T_0} \\ nc_V&=\frac{3P_{I_0} A_cL}{4T_0} \\ nc_V&\approx1.48 ~ \text{J/K}. \end{split} $$

Para determinar la temperatura $T_1$ aprovecharemos la igualdad $$ \frac{P_{I_1} V_1}{T_1}= \frac{P_{I_0} V_0}{T_0}, $$

y que $P_{I_1} V1^{\gamma} = P_{I_0} V_0^{\gamma}$,

$$ \begin{split} T_1 &= \frac{P_{I_1} V_1}{P_{I_0} V_0} T_0\\ &= \frac{P_{I_1}}{P_{I_0}} \left(\frac{P_{I_0}}{P_{I_1}} \right)^{\frac{1}{\gamma}} T_0 \\ &= \left(\frac{P_{I_1}}{P_{I_0}} \right)^{\frac{\gamma-1}{\gamma}} T_0 \\ &= \left(\frac{P_{I_1}}{P_{I_0}} \right)^{\frac{2}{5}} T_0 \\ T_1 & \approx 288 ~ K = 14.85^{\circ}\text{C} \\ \end{split} $$

Volviendo a la ecuación (5) podemos obtener que $\boxed{T \approx 94.99^{\circ}\text{C}}$. Luego, aprovechando nuevamente la constancia en la cantidad de moles y que el volumen final del gas es $V_1$, podemos plantear la igualdad

$$ \frac{P_{I_1}}{T_1} = \frac{P}{T} $$ es decir,

$$ P= \frac{T}{T_1} P_{I_1} , $$

es decir, $P \approx 1.53 \cdot 10^5 ~ \text{Pa}$.