N°02-2024

Enunciado

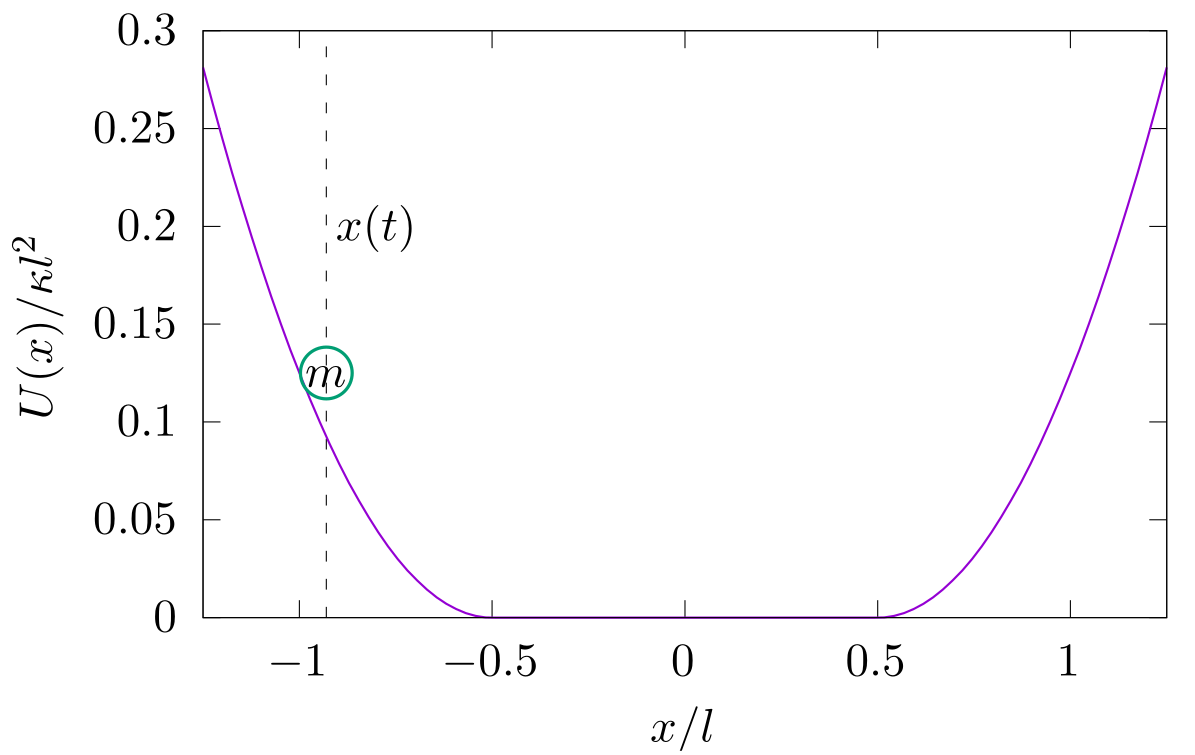
Despreciando efectos de rozamiento, calcular el período de oscilación $T$ de una partícula de masa $m$ en un potencial $$ U(x)= \begin{cases} \begin{split} & \frac{1}{2} \kappa \left( |x| - \frac{l}{2} \right)^2 ~~~~~ |x|> \frac{l}{2} \\ & 0 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ |x|\leq \frac{l}{2} \end{split} \end{cases} $$ en función de su energía $E$.

a) ¿A qué tiende el resultado cuando $E\gg \kappa l^2$? Interpretar.
b) ¿A qué tiende el resultado cuando $E\ll \kappa l^2$? Interpretar.
c) Si se denomina $x(t)$ a la posición de la partícula a tiempo $t$, y $p(t)$ a su momento lineal a tiempo $t$, realizar un gráfico bidimensional de la curva paramétrica $(x(t), p(t))$ para $0 \leq t \leq T$ .

Resolución

Intentemos entender qué tipo de interacción proviene del potencial, para ello tengamos en cuenta que la fuerza estará dada por $F(x)=-\frac{dU(x)}{dx}$, entonces $$ F(x)= \begin{cases} \begin{split} & - \kappa \left( x + \frac{l}{2} \right) ~~~~~~~~~ x<- \frac{l}{2} \\ & 0 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ |x|\leq \frac{l}{2} \\ & - \kappa \left( x - \frac{l}{2} \right) ~~~~~~~~~ ~ x> \frac{l}{2} \end{split} \end{cases}. $$

Analizando la estructura de la fuerza, en lugar de la estructura de la energía potencial, es más sencillo identificar que para $x<- \frac{l}{2}$ y $x> \frac{l}{2}$ se trata de un movimiento armónico de período

$$ T_{arm}= 2 \pi \sqrt{\frac{m}{\kappa}}. ~~~~~~~~~~(1) $$

Tal oscilación es interrumpida por un movimiento intermedio a velocidad constante en el intervalo $\left[-\frac{l}{2},+\frac{l}{2} \right]$. El tiempo que la partícula permanece en tal región esta dado por $$ T_{int} = \frac{2l}{v}, $$ donde $v$ es la velocidad a la que se mueve. Podemos obtener ésta última a través de la conservación de la energía. Si la energía mecánica total es $E$, entonces, dado que la energía potencial en la región intermedia es nula, tenemos que

$$ E = \frac{1}{2} m v^2 \Rightarrow v = \sqrt{\frac{2E}{m}}, $$

y por lo tanto

$$ T_{int} = l \sqrt{\frac{2m}{E}}. ~~~~~~~~~~(2) $$

El período del movimiento estará dado por la suma $T = T_{arm}+T_{int}$, de manera que sumando las relaciones (1) y (2) obtenemos:

$$ \boxed{T=2 \pi \sqrt{\frac{m}{\kappa}}+l \sqrt{\frac{2m}{E}}}. $$

Para las siguientes preguntas podemos definir $\alpha$ tal que $E=\alpha \kappa l^2$ y reexpresar convenientemente el período.

a)

En este caso podemos escribir $$ T=2 \pi \sqrt{\frac{ m}{\kappa}}+ \sqrt{\frac{2m}{\alpha \kappa}}. $$

Si $E \gg \kappa l^2$, entonce $\alpha \gg 1 $ y por lo tanto $T\approx 2 \pi \sqrt{\frac{ m}{\kappa}}$. Es decir, la energía es tan grande que el tiempo de permanencia en la región $\left[-\frac{l}{2},+\frac{l}{2} \right]$ es despreciable respecto el tiempo en el que oscila.

b)

Para este otro caso podemos escribir $$ T=2 \pi l \sqrt{\frac{\alpha m}{E}}+l \sqrt{\frac{2m}{E}}. $$

Si $E\ll \kappa l^2$, entonces $\alpha \ll 1 $ y por lo tanto $T\approx l \sqrt{\frac{2m}{E}}$. Es decir, la energía es tan pequeña que el tiempo de permanencia en la región $\left[-\frac{l}{2},+\frac{l}{2} \right]$ es muy grande respecto el tiempo de oscilación.

¿Cómo se te ocurrió definir $\alpha$ para analizar los límites?

Fue motivado por auspiciantes que han realizado su aporte libre y voluntario. ¡Gracias!. Hablando en serio, la prolijidad de análisis que permite la introducción del factor $\alpha$ hace una gran diferencia cuando se realizan experimentos y es necesario tener una noción precisa de la interrelación entre los parámetros que caracterizan al fenómeno. Cuando los parámetros son de diferente índole (energía, distancia, constante elástica, lo que se te ocurra, etc), la introducción de parámetros secundarios adimensionales que los vincule da oportunidad a que las relaciones manifiesten más claramente su estructura.

Por ejemplo, en a) y b), los dos términos que determinan el período son claramente de la misma índole: son factores de $\sqrt{\frac{ m}{\kappa}}$ en el primer caso y de $l \sqrt{\frac{m}{E}}$ en el segundo. Así, es natural poder despreciar un término respecto de otro cuando comparten una estructura evidente. Además, es menos problemático analizar los límites cuándo un numero adimensional es mucho más grande o mucho más chico que $1$.

A un nivel de análisis de errores de las magnitudes, al realizar un experimento, $\alpha$ nos ayudaría a ser más conscientes de cómo son los términos respecto de los errores de medición (directa o indirecta) del período. En el arte de realizar experimentos y procesar su información, procedimientos como estos tienen un contenido y una carga fuertemente moral: porque un análisis incorrecto puede provocar situaciones peligrosas a un nivel tecnológico o a que un funcionario tome malas decisiones como el caso de un juez que se basa en una pericia de física forense.

c)

Para este inciso podemos aprovechar la conservación de la energía mecánica. Si $T=\frac{p^2}{2m}$ es la energía cinética, como se debe cumplir que $E=T+U$, la estructura de la energía potencial impacta en la conservación de la siguiente forma

$$ \begin{cases} \begin{split} & \frac{p^2}{2m}+\frac{1}{2} \kappa \left( |x| - \frac{l}{2} \right)^2 =E~~~~~ |x|> \frac{l}{2} \\ & \frac{p^2}{2m} = E~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ |x|\leq \frac{l}{2} \end{split} \end{cases} $$

que organizando y separando un poco se convierte en

$$ \begin{cases} \begin{split} & \frac{p^2}{2mE}+\frac{\left( x + \frac{l}{2} \right)^2}{2E/\kappa} =1,~~~~~ x<- \frac{l}{2} \\ & p = \pm \sqrt{2mE}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ |x|\leq \frac{l}{2} \\ & \frac{p^2}{2mE}+\frac{\left( x - \frac{l}{2} \right)^2}{2E/\kappa}=1,~~~~~ x> \frac{l}{2} \end{split} \end{cases} $$

donde vemos que para $x<- \frac{l}{2}$ tenemos la mitad de una elipse centrada en $- \frac{l}{2}$ cuyos semiejes son $\sqrt{2mE}$ y $\sqrt{2E\kappa}$. Algo totalmente simétrico sucede para $x>\frac{l}{2}$. Para al región $\left[-\frac{l}{2},+\frac{l}{2} \right]$ tenemos dos rectas horizontales en $\pm \sqrt{2mE}$.

Una representación de la curva $(x,p)$ puede verse a continuación en la (Figura A).