N°01-2024

Enunciado

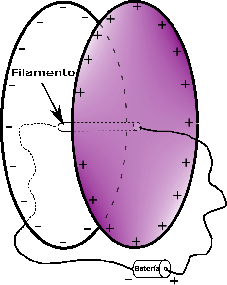
Se tiene un instrumento que consiste en dos discos conductores de radio $r$, separados por $d = 1~\text{cm}$. El sistema posee una capacidad eléctrica de $C = 1 \mu F$. Estos discos no están completamente aislados entre sı́, sino que un filamento de sección transversal $s = 10^{-6} cm^2$ los conecta justo en el centro, como se muestra en la figura. El filamento posee una resistividad eléctrica de $\rho = 3 \cdot 10^{-8} ~\Omega m$. Se aplica una tensión eléctrica entre ambos discos, de manera tal que éstos se cargan eléctricamente, y se atraen.

Calcular la corriente que circula por el filamento cuando el mismo soporta una tensión de compresión de $100~Pa$. Para calcular el campo eléctrico entre los discos puede suponer que éstos se comportan como planos infinitos con densidad de carga uniforme. Se supone que la longitud del filamento permanece constante.

Resolución

Equilibrio sobre el filamento

Consideremos el balance de fuerzas sobre el filamento (Figura A), en el que ambos discos ejercen la misma fuerza de contacto $F$ bajo la presión $p=100~Pa$ sobre la superficie $s$, de manera que

$$ F = ps. ~~~~~~~~ (1) $$

Equilibrio sobre los discos

En el caso de los discos (usemos como ejemplo el disco izquierdo como muestra la Figura B), además de actuar la correspondiente reacción a la fuerza de contacto con el filamento, actúa a fuerza de atracción $F_A$ entre ellos. Tal fuerza está dada por la carga $Q$ del disco en cuestión y el campo $E_1$ generado por el otro disco, es decir, $F_A=QE_1$. La carga se puede escribir en términos de la capacitancia $C$ y la diferencia de potencial $V$, $Q=CV$. El campo generado por un disco es la mitad del campo total $E$ en el capacitor, que a su vez puede expresarse en términos de la diferencia de potencial y la distancia $d$ entre los discos, $E=V/d$. Así, tendremos que

$$ \begin{split} F_A&= Q E_1\\ &= (CV)(\frac{E}{2})\\ &= (CV)(\frac{V}{2d}), \end{split} $$

es decir,

$$ F_A =\frac{CV^2}{2d}. ~~~~~~~~ (2) $$

Diferencia de potencial entre las placas

A partir de las relaciones (1) y (2), ya que se debe cumplir que $F_A=F$, podemos obtener la diferencia de potencial entre las placas

$$ \begin{split} F_A&= F\\ \frac{CV^2}{2d}&= ps\\ CV^2&= 2dps\\ V^2&= \frac{2dps}{C} \end{split} $$ es decir, $$ V = \sqrt{\frac{2dps}{C}}. ~~~~~~~~ (3) $$

Corriente por el filamento

Por la ley de Ohm, la corriente por el filamento estará dada por $I=V/R$ donde la resistencia $R$ del filamento puede expresarse en términos de su geometría y su resistividad $\rho$ como

$$ R = \rho \frac{d}{s}, $$

y por lo tanto, usando también la relación (3), resulta que

$$ \boxed{I= \frac{1}{\rho}\sqrt{\frac{2ps^3}{dC}}}. $$

Hay personas que llegan a una relación completamente análoga, pero sin el factor $2$ en al raíz. Eso se debe a que no han realizado su aporte libre y voluntario.¡Gracias!. Hablando en serio, se debe a que han usado el campo total $E$ para calcular la fuerza $F_A$ que un disco hace sobre otro. Pero, como vimos, en ese caso debemos usar el campo $E_1$ que genera una sola placa.

Como $s = 10^{-6} cm^2 = 10^{-10} m^2$, $d = 1~\text{cm}= 0.01~\text{m}$

$$ \begin{split} I=& \frac{1}{3 \cdot 10^{-8} ~ \Omega m}\sqrt{\frac{2 \cdot 100 ~ Pa \cdot. (10^{-10} m^2)^3}{ 0.01 ~ \text{m} \cdot 1 \mu F}}\\ =& \frac{1}{3 \cdot 10^{-8} ~\Omega m}\sqrt{2 \cdot 10^{-20}\frac{ ~ Pa ~ m^5}{F}} \end{split} $$

Como $Pa~m^3= N m =J = C V$ y $F=C/V$:

$$ \begin{split} I=& \frac{1}{3 \cdot 10^8 ~ \Omega m}\sqrt{2 \cdot 10^{-20} ~ V^2 ~ m^2} \\ =& \frac{\sqrt{2} \cdot 10^{-10} ~ V ~ m}{3 \cdot 10^{-8} ~ \Omega m} \\ =& \frac{\sqrt{2}}{3} \cdot 10^{-2} V/\Omega \\ =& \frac{\sqrt{2}}{3} \cdot 10^{-2} ~ A \\ =& \frac{10\sqrt{2}}{3} ~ mA \\ \end{split} $$

es decir, $\boxed{I \approx 4,7~mA}$.