N°12-2023
Enunciado
Considere el circuito de la figura, con dos inductancias idénticas de valor $L$ y tres capacitores idénticos con capacitancia $C$. No hay disipación. Inicialmente todos los capacitores están cargados arbitrariamente y se deja evolucionar el sistema.
Demuestre que tanto la suma como la resta de las cargas en los capacitores laterales realizan oscilaciones armónicas en función del tiempo, pero con distintas frecuencias. Determine estas dos frecuencias en función de los parámetros del circuito.
Resolución
Realicemos un análisis en las dos mayas suponiendo que las corrientes tienen el sentido representado en el esquema de la Figura A. En ese caso, cuando el capacitor de la izquierda tiene una carga $Q_1$, por él circula una corriente $I_1=\frac{dQ_1}{dt}$. Análogamente, si $Q_2$ es la carga en el capacitor de la derecha, por él circula una corriente $I_2=\frac{dQ_2}{dt}$. Como por el capacitor del centro circula una corriente $I_{12}=I_1-I_2=\frac{d(Q_1-Q_2)}{dt}$, podemos decir que su carga coincide con $Q_1-Q_2$ a menos de una constante, es decir, $Q_{12}^{-}=Q_1-Q_2+q$ con $\frac{dq}{dt}=0$.
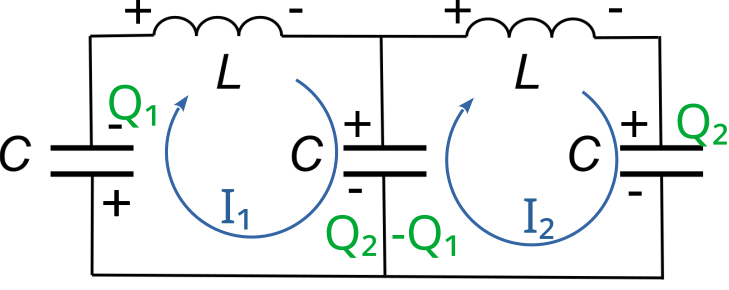
Figura A
Las ecuaciones para cada una de las mayas son:
$$ \begin{cases} \begin{split} -\frac{Q_1}{C}-L\frac{dI_1}{dt}-\frac{Q_{12}^{-}}{C}=& 0 ~~~~~~\text{(Malla izquierda)}\\ \frac{Q_{12}^{-}}{C}-L\frac{dI_2}{dt}-\frac{Q_2}{C}=& 0 ~~~~~~\text{(Malla derecha)} \end{split} \end{cases} $$
es decir,
$$ \begin{cases} \begin{split} -\frac{Q_1}{C}-L\frac{d^2Q_1}{dt^2}-\frac{Q_{12}^{-}}{C}=& 0 \\ \frac{Q_{12}^{-}}{C}-L\frac{d^2Q_2}{dt^2}-\frac{Q_2}{C}=& 0. \end{split} \end{cases} $$
Si sumamos y restamos estas ecuaciones podemos obtener lo siguiente $$ \begin{cases} \begin{split} \frac{Q_1+Q_2}{C}+L\frac{d^2(Q_1+Q_2)}{dt^2}=& 0 \\ 2\frac{Q_{12}^{-}}{C}+L\frac{d^2(Q_1-Q_2)}{dt^2}+\frac{Q_1-Q_2}{C}=& 0. \end{split} \end{cases} $$
Como $Q_{12}^{-}=Q_1-Q_2+q$ y $\frac{d^2(Q_1-Q_2)}{dt^2}=\frac{d^2Q_{12}^{-}}{dt^2}$, si además definimos $Q_{12}^{+}=Q_1+Q_2$ y acomodamos un poco las cosas:
$$ \begin{cases} \begin{split} \frac{1}{LC}Q_{12}^{+}+\frac{d^2Q_{12}^{+}}{dt^2}=& 0 \\ 3\frac{1}{LC} Q_{12}^{-}+\frac{d^2Q_{12}^{-}}{dt^2}=& -\frac{q}{LC}. \end{split} \end{cases} $$
Estos resultados pueden interpretarse como un sistema de osciladores cuyas frecuencias de vibración están dadas por
$$ \boxed{ \begin{split} \omega_{-}^2 =&\frac{1}{LC}\\ \omega_{+}^2 =&3 \omega_{-}^2 \end{split} }. $$