N°06-2023
Enunciado
Una esfera maciza y homogénea de masa $m$ y radio $R$ se encuentra flotando en un líquido de densidad $\rho$.
Si la parte de la esfera que sobresale del agua tiene una altura $h=R/2$, determine la densidad $\rho$ del líquido en función de $m$ y $R$.
Describa cualitativamente qué sucede con la esfera si se le aplica una fuerza impulsiva (de corta duración) como indica la figura (desprecie los efectos de rozamiento).
Resolución
1.
En el balance de fuerzas sobre la esfera intervienen las fuerzas peso $mg$ y de empuje $B$:
$$ \sum F = B-mg $$
La fuerza de empuje puede expresarse en términos de la densidad $\rho$ del líquido y el volumen sumergido $V_s(h)$ como
$$ B(h) = \rho g V_s(h) $$
donde estamos expresando la dependencia de las magnitudes con la altura $h$ que sobresale la esfera.
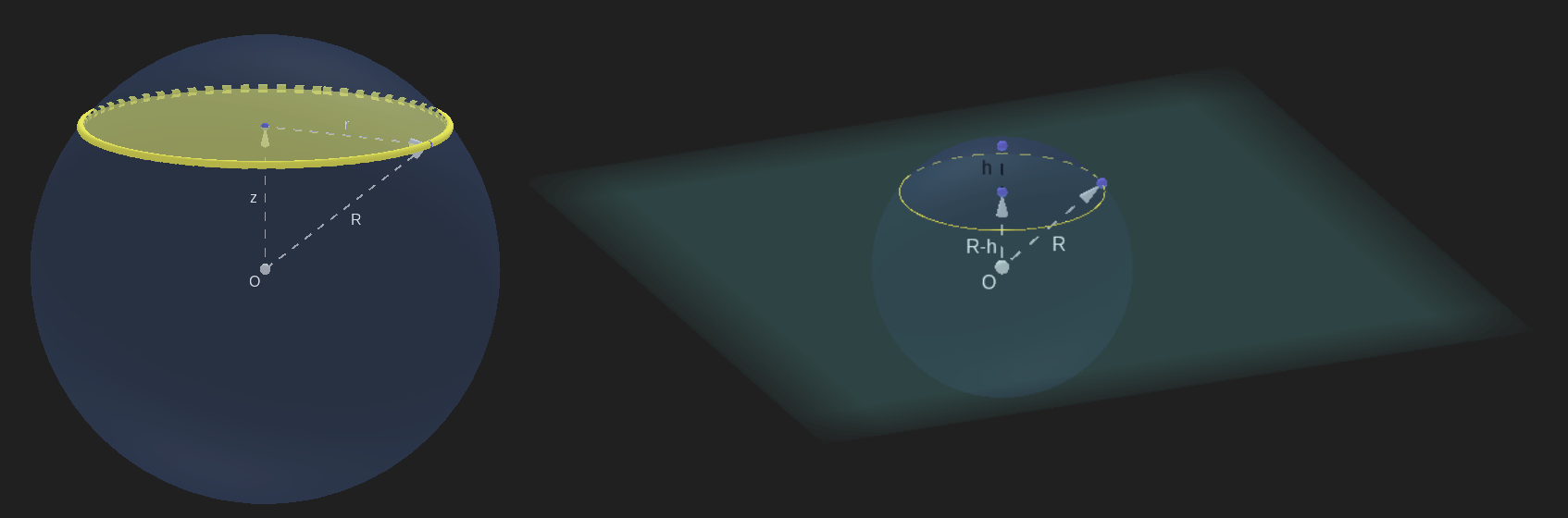
Figura A
Veamos cómo determinar el volumen $V_s(h)$ sumando discos horizontales de radio $r$ en la posición vertical $z$ respecto del centro de la esfera (imagen izquierda de la Figura A). La altura de los discos varía desde el valor $-R$ hasta $R-h$ (imagen derecha de la Figura A) Cada disco tiene un volumen elemental $dV = \pi r^2 dz$ y, a su vez, $r^2=R^2-z^2$ entonces
$$ \begin{split} V_s(h) =& \int_{-R}^{R-h} \pi (R^2-z^2)dz \\ =& \pi \left[ R^2 z-\frac{z^3}{3} \right]_{-R}^{R-h} \\ =& \pi \left[ R^2 (R-h)-\frac{(R-h)^3}{3} + R^3 - \frac{R^3}{3} \right]_{-R}^{R-h} \\ =& \pi \left[ \frac{5}{3} R^3 -R^2h-\frac{(R-h)^3}{3} \right], \end{split} $$
que cuando $h=R/2$,
$$ \begin{split} V_s(R/2) =& \pi \left[ \frac{5}{3} R^3 -R^2h-\frac{(R-h)^3}{3} \right] \\ =& \pi \left[ \frac{5}{3} R^3 -\frac{1}{2} R^3-\frac{1}{24} R^3 \right] \\ =& \pi \left[ \frac{40-12-1}{24} \right] R^3 \\ =& \pi \frac{27}{24} R^3, \end{split} $$
es decir,
$$ V_s(R/2) = \frac{9}{8} \pi R^3. $$
Así, cuando el cuerpo se encuentra en equilibrio el peso y el empuje son iguales y por lo tanto:
$$ \begin{split} B(R/2) &= mg \\ \rho g V_s(R/2) &= mg \\ \rho \frac{9}{8} \pi R^3 &= m \end{split} $$
y por lo tanto
$$ \boxed{\rho = \frac{8m}{9\pi R^3}}. $$
2.
Movimiento del centro de masas
Cuando la fuerza $F$ se ejerce durante un intervalo de tiempo $\Delta t$, produce una cantidad de movimiento en la dirección vertical igual a $p= F \Delta t$ que generará que el centro de masas comience a descender de forma desacelerada (ya que $B>mg$) hasta detenerse. Luego comenzará a subir de forma acelerada hasta la posición de equilibrio y de forma desacelerada cuando la sobrepase ($B<mg$). El final en el movimiento de subida dependerá de la cantidad de movimiento que haya producido la fuerza y el tiempo que fué aplicada: pudiendo subir hasta regresar nuevamente sin salir completamente del agua ó saliendo de ella volando por el aire hasta sumergirse nuevamente luego de un tiempo. En ambos casos la esfera regresa a su condición inicial para repetir su movimiento periódicamente. Esta oscilación no es lineal, por la dependencia del empuje con la profundidad.
Rotación
En cuanto al aspecto angular, la fuerza produce un torque que genera un momento angular y, por lo tanto, una velocidad angular. Luego del impacto el torque es nulo y tanto el momento como la velocidad angular permanecen constantes.
Así, la esfera adquiere un movimiento compuesto que consiste en un movimiento de giro a velocidad angular constante y un movimiento oscilatorio (no armónico) de su centro de masas.