N°03-2023
Enunciado
Determine el campo eléctrico sobre el eje de simetría de un anillo de radio $R$ y densidad lineal de carga uniforme $\lambda$.
Haga un gráfico cualitativo de la función obtenida, para puntos situados sobre el eje y hasta $3R$ del centro del anillo. Indique claramente el sistema de coordenadas utilizado para describir el problema.
Determine el campo eléctrico sobre el eje de simetría de un disco plano de radio $R$ y densidad superficial de carga $\sigma$.
Considere ahora que el disco plano es envuelto por un conductor esférico de carga total $Q$, espesor despreciable y radio $2R$, cuyo centro coincide con el centro del disco. Indique cuál es el valor del campo eléctrico sobre el eje de simetría del disco a una distancia $3R$ del centro del mismo.
Resolución
1.
Consideremos un elemento de carga $dQ$ correspondiente a un elemento de arco $dl$ (Figura A). El campo eléctrico $d \overline{E}$ que produce en un punto sobre el eje de simetría ubicado a la distancia $z$ de su centro tiene la siguiente magnitud:
$$ dE= k \frac{dQ}{r^2}. $$
Como el elemento de carga se puede expresar como $dQ=\lambda dl$, la longitud de arco como $dl= R d \theta$ y $r = \sqrt{z^2+R^2}$:
$$ dE= k \frac{\lambda R}{z^2+R^2} d \theta ~~~~~~~~ (1). $$
Por otro lado, la dirección del campo $d \overline{E}$ se puede caracterizar por el ángulo $\phi$ que subtiende con el eje de simetría del anillo (Figura A) que a su vez puede calcularse a traves de la siguiente relación trigonométrica
$$ \cos \phi = \frac{z}{r} = \frac{z}{\sqrt{z^2+R^2}} ~~~~~~~~ (2). $$
Figura A
Un anillo cargado de radio $R$ crea un campo eléctrico que puede concebirse como la superposición de los campos generados por elementos de carga localizados en elementos de longitud de arco $dl$, el cuál subtiende un ángulo $d\theta$ respecto del centro del anillo. Un punto ubicado sobre el eje de simetría a la distancia $z$ del centro, dista una distancia $r=\sqrt{z^2+R^2}$ con el elemento de carga. El campo $d \overline{E}$ que el mismo genera en tal punto subtiende un ángulo $\phi$ con el eje de simetría.
Luego, podemos tener en cuenta que por cada elemento de carga $dQ$ existirá siempre un elemento de carga diametralmente opuesto y cuyo campo tiene la misma componente a lo largo de eje de simetría, pero que a su vez tiene una componente contraria en el plano perpendicular a tal eje. La suma de tales campos tendrá como resultante un campo en la dirección del eje de simetría. Así, el campo total estará conformado sólo por las contribuciones en la dirección del eje de simetría. Si integramos esta idea a todo el anillo $\mathcal{C}$, resulta que el módulo del campo total estará constituido por todas las contribuciones $dE_z= dE \cos \phi$:
$$ E= \int_{\mathcal{C}} d E_z= \int_{\mathcal{C}} dE \cos \phi. $$
Si tenemos en cuenta las relaciones (1) y (2):
$$ \begin{split} E &=\int_{0}^{2\pi} k \frac{\lambda R}{z^2+R^2} \cos \phi ~ d \theta \\ &=\int_{0}^{2\pi} k \frac{\lambda z R}{(z^2+R^2)^{3/2}} ~ d \theta \end{split} $$
donde vemos que el integrando es independiente de $\theta$ (lo cuál es razonable por la simetría) y por lo tanto:
$$ \boxed{E(z) = k \lambda 2\pi R \frac{z}{(z^2+R^2)^{3/2}} }. ~~~~~~~~ (3) $$
2.
Para graficar la dependencia expresada en la relación (3) podemos reconocer que $E(0)=0$ y que $\lim_{z \to \pm \infty} E(z)= 0$. Así, como en el campo es nulo en el origen, tiende a cero cuando se aleja hacia el infinito y la dependencia no es la función trivialmente nula: es de esperar que tenga extremos para algún par de valores de $z$. Para obtener los puntos críticos correspondiente tenemos que
$$ \left. \frac{d E}{d z} \right|_{z_c}= 0 \Leftrightarrow \left. \frac{d}{d z} \left( \frac{z}{(z^2+R^2)^{3/2}} \right) \right|_{z_c} = 0, $$
y por lo tanto
$$ \begin{split} 0=&\frac{1}{(z_c^2+R^2)^{3/2}} - \frac{3 z_c^2}{(z_c^2+R^2)^{5/2}} \\ 0=&\frac{1}{(z_c^2+R^2)^{3/2}} - \frac{3 z_c^2}{(z_c^2+R^2)^{3/2}} \\ 0=&\frac{z_c^2+R^2-3z_c^2}{(z_c^2+R^2)^{3/2}} \\ 0=&\frac{R^2-2z_c^2}{(z_c^2+R^2)^{3/2}} \\ 0=& R^2-2z_c^2 \\ z_c =& \frac{R}{\sqrt{2}}. \end{split} $$
Para graficar la dependencia puede ayudarnos adimensionalizar las variables de la relación (3). Por ejemplo, podemos adimensionalizar $z$ dividiéndolo por $R$ y reorganizando para adimensionalizar el campo eléctrico:
$$ \frac{E(z)}{k \lambda 2\pi/ R} = \frac{z/R}{[(z/R)^2+1]^{3/2}} ~~~~~~~~ (3). $$
En la Figura B tenemos una representación de tal dependencia donde se especifican los puntos críticos y sus correspondientes extremos.
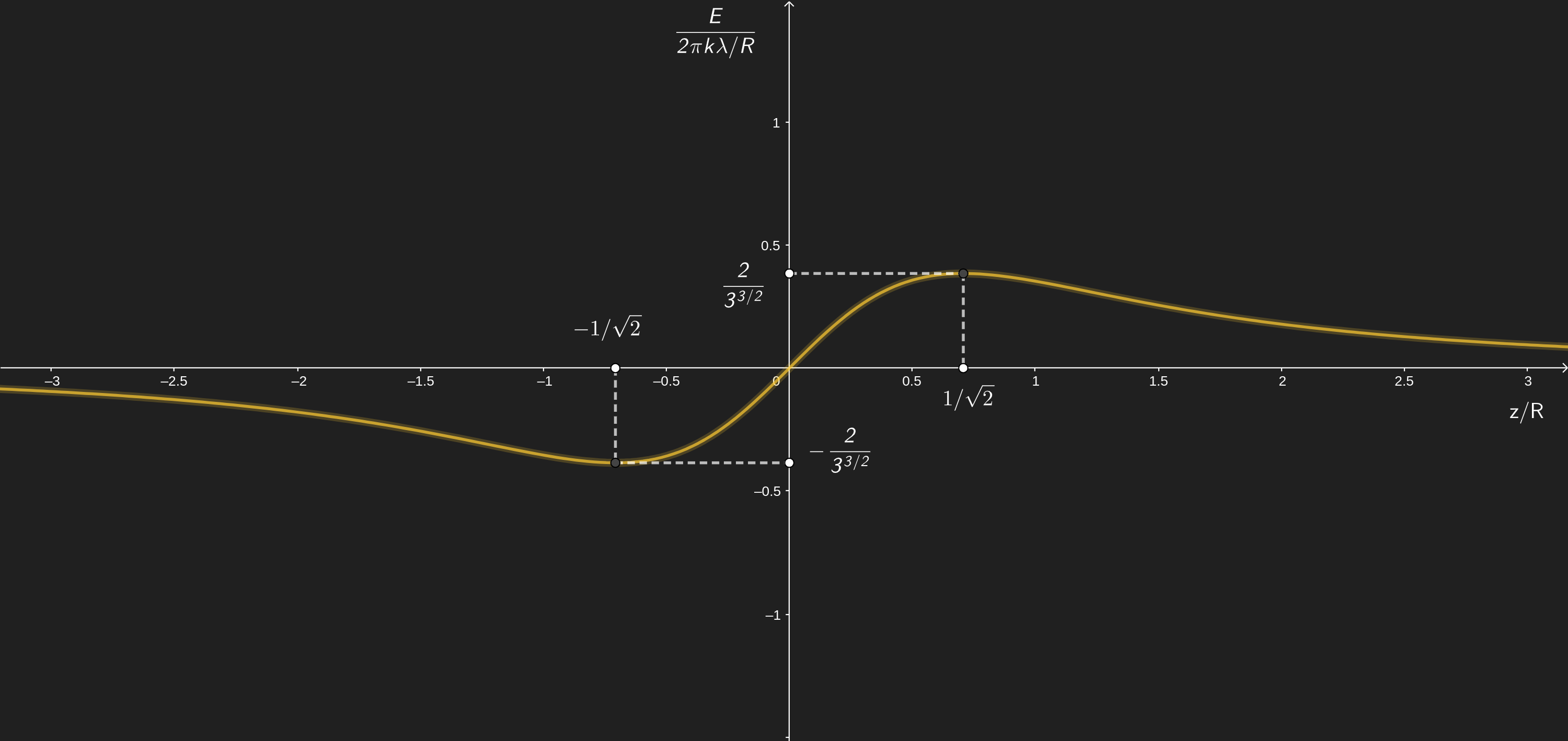
Figura B
Dependencia entre el campo eléctrico generado por un anillo de radio $R$ dotado con una densidad lineal de carga $\lambda$ y la distancia $z$ desde el centro a un punto ubicado sobre el eje de simetría. En los ejes cartesianos representan tales magnitudes adimensionalizadas. Se observa como el campo es nulo en el origen, aumenta en valor absoluto hasta llegar a un valor máximo y luego empieza a decaer tendiendo a cero en distancias suficientemente grandes.
3.
Podemos pensar al disco como un continuo de anillos elementales de radio $r$ y espesor $dr$ (Figura C). Así, determinando el campo que genera cada anillo elemental podemos realizar una integración para obtener el campo generado por el disco.
Figura C
Para determinar el campo eléctrico producido por un disco de radio $R$ cargado uniformemente se puede determinar el campo generado por un anillo de radio $r<R$ y espesor $dr$ para luego integrar.
Comencemos reexpresando el campo dado por la relación (3) teniendo en cuenta que la carga total del anillo es $q=\lambda 2 \pi r$:
$$ E_{\text{anillo}}(z) = k q \frac{z}{(z^2+r^2)^{3/2}}. $$
De manera que cada anillo elemental produce un campo dado por
$$ dE(z) = k d q \frac{z}{(z^2+r^2)^{3/2}}, $$
donde $dq = \sigma d S$ y $dS= 2 \pi r dr$, entonces
$$ dE(z) = k \sigma 2 \pi r dr \frac{z}{(z^2+r^2)^{3/2}} ~~~~~~~~ (4). $$
Si integramos y reorganizamos un poco:
$$ \begin{split} E(z)=&\int_0^R dE(z) \\ =& 2 \pi k \sigma z \int_0^R \frac{r dr}{(z^2+r^2)^{3/2}}. \end{split} $$
Para realizar la integral podemos definir $u=z^2+r^2$, de manera que $du=2rdr$ y por lo tanto: $$ \begin{split} E(z)=& \pi k \sigma z \int_{z^2}^{z^2+R^2} \frac{du}{u^{3/2}} \\ =& \pi k \sigma z \left( -2u^{-1/2}\right) \left. \right|_{z^2}^{z^2+R^2} \\ =& 2 \pi k \sigma z \left( \frac{1}{|z|} - \frac{1}{\sqrt{z^2+R^2}}\right) \\ =& 2 \pi k \sigma \left( \frac{z}{|z|} - \frac{z}{\sqrt{z^2+R^2}}\right) ~~~~~~~~ (5). \end{split} $$
Aquí vemos que esta expresión no puede ser válida para $z=0$, sino que para ello debemos identificar en la relación (4) que todas las contribuciones de los anillos elementales son nulas y por lo tanto el campo total también lo es. Una forma más elegante de expresar el campo obtenido, es utilizando la función signo $\mathrm{sgn}$ definida como
$$ \mathrm{sgn} \equiv \begin{cases} \begin{split} -1 &\text{ si } x < 0, \\ 0 &\text{ si } x = 0, \\ 1 &\text{ si } x > 0. \end{split} \end{cases} $$
Cuando $x \neq 0$ se puede escribir $\mathrm{sgn} (x)= x/|x|$, entonces podemos volver a la relación (5) para expresar el campo para cualquier $z$, incluido $z=0$, como
$$ \boxed{E(z) = 2 \pi k \sigma \left( \mathrm{sgn} (z) - \frac{z}{\sqrt{z^2+R^2}}\right)}. $$
4.
Cuando cualquier distribución de carga se encuentra dentro de una cascara conductora, la carga inducida en su pared interna se distribuye de manera tal que en conjunto producen un campo eléctrico nulo en el exterior de la cascara. Así, el campo eléctrico en la región externa estará dado sólo por la carga distribuida en la superficie exterior de la cáscara conductora. Te invito a visitar y leer atentamente el artículo denominado Propiedades de una cáscara conductora que escribí específicamente para demostrar estas propiedades.
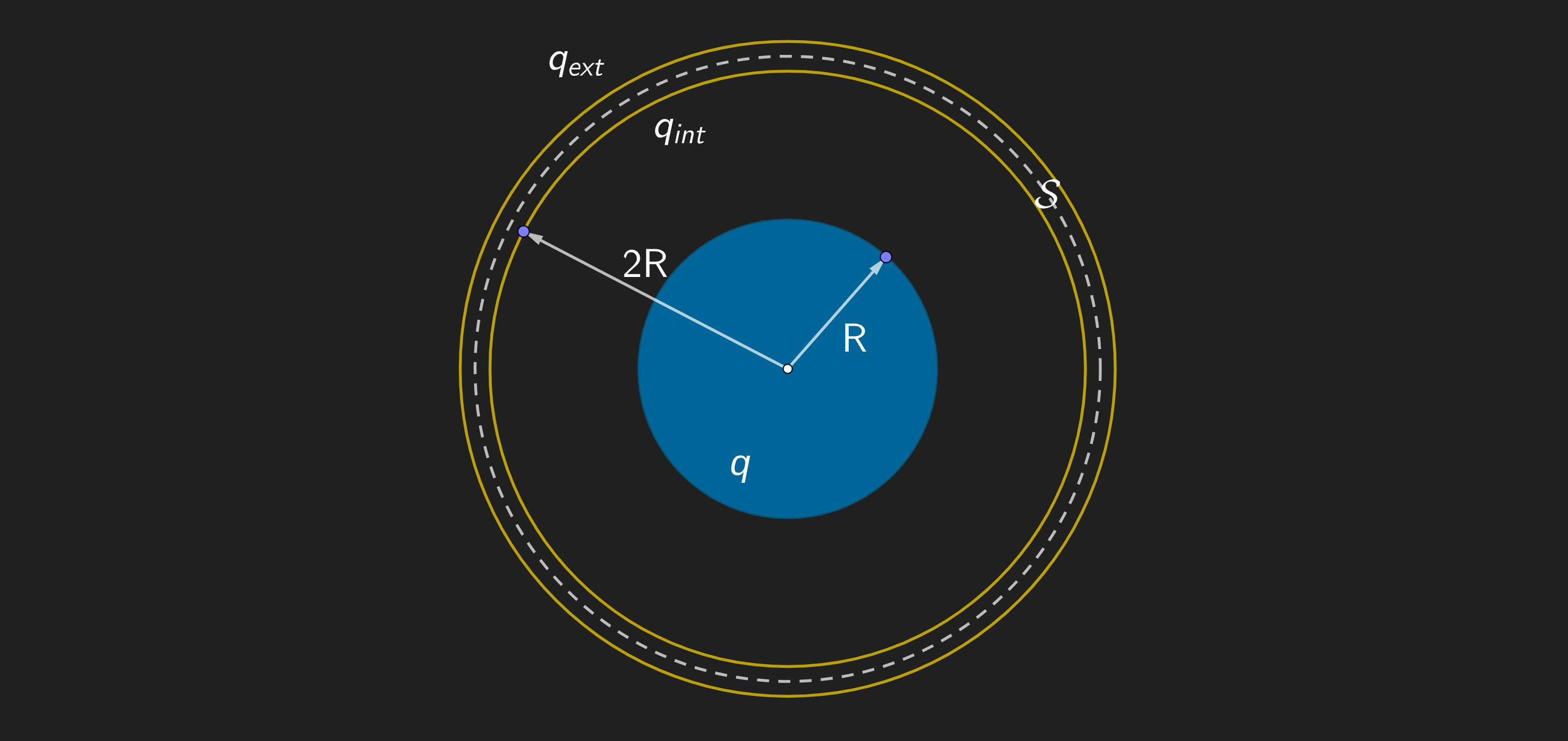
Figura D
Un disco de radio $R$ cargado eléctricamente con una carga $q$ se encuentra en el hueco de un conductor esférico de radio $2R$. El dibujo representa un corte plano que contiene al disco. Éste último induce una distribución de carga $q_{\text{int}}$ en la pared interior. Para determinarla, es posible aplicar el teorema de Gauss a una superficie $\mathcal{S}$ que se distribuye por el interior del conductor, donde el campo eléctrico es nulo. Gracias a la misma idea también es posible obtener la carga $q_{\text{ext}}$ distribuida en la superficie externa.
En fin, debemos determinar la distribución de carga en la superficie exterior y luego determinar el campo que la misma genera. Para ello usaremos el teorema de Gauss en una superficie $\mathcal{S}$ interna al conductor Figura D, donde el campo eléctrico es cero. Así, el flujo de este último también es cero y, por lo tanto, también lo es la carga encerrada por la superficie. Es decir, la suma de la carga $q_{\text{int}}$ distribuida en la superficie interna del conductor con la carga $q=\sigma \pi R^2$ del disco, debe ser cero y por lo tanto
$$ q_{\text{int}} = -q = - \sigma \pi R^2. $$
Como el conductor tiene una carga $Q=q_{\text{int}}+q_{\text{ext}}$, entonces la carga distribuida en la superficie exterior es
$$ q_{\text{ext}}=Q-q_{\text{int}} = Q + \sigma \pi R^2. ~~~~~~~~ (6) $$
Finalmente, como el campo exterior producido conjuntamente por el disco y la carga distribuida en la superficie interna es nulo, en la superficie externa la carga se distribuye simétricamente. Es decir, la carga externa $q_{\text{ext}}$ se distribuye uniformemente y, como bien es sabido, para $r>2R$ genera un campo eléctrico equivalente al de una carga puntual de igual magnitud ubicada en el centro de la esfera:
$$ E(r) = k \frac{q_{\text{ext}}}{r^2}. $$
Así, usando lo obtenido en la relación (6) podemos obtener el campo a la distancia $r=3R$:
$$ \boxed{E(3R) = k \frac{Q + \sigma \pi R^2}{9 R^2}}. $$
Algo interesante de este resultado, y de la argumentación necesaria para llegar a él, es que el campo es el mismo para cualquier punto ubicado a la distancia $3R$, no solamente si esta ubicado en el eje de simetría. Esto se debe a que el campo eléctrico en el exterior tiene simetría esférica, a pesar de la simetría cilíndrica de la distribución de cargas en la cavidad.
Ojala te quede claro el desarrollo de este problema. Si está en tus posibilidades y valoras lo expuesto, te agradecería que me ayudes con un aporte libre y voluntario.