N°09-2022
Enunciado
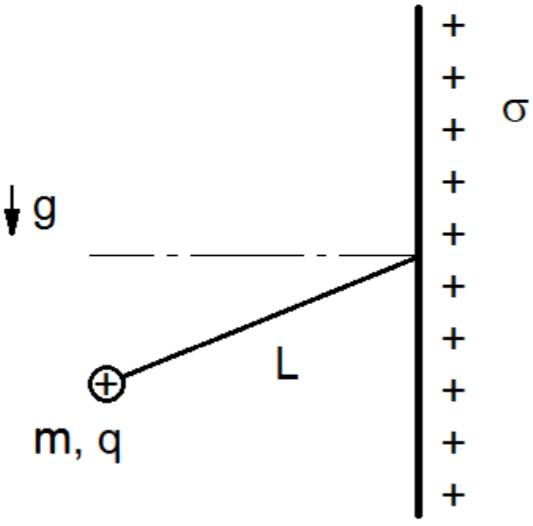
Se tiene un plano infinito, con una densidad de carga uniforme $\sigma$ en presencia de un campo gravitatorio como indica la figura. En un punto del plano se fija un hilo de longitud $L$. En el otro extremo del hilo se sujeta una partícula de masa $m$ y carga $q$. Los signos de $\sigma$ y $q$ son iguales.
- En equilibrio estático, ¿qué ángulo forma el hilo con la normal al plano?
- Se aparta la masa del punto de equilibrio un pequeño ángulo en dirección tangencial al hilo en el plano del papel, y se la suelta. ¿Con qué período oscila la masa?
- ¿Cambia el período si el apartamiento es en la dirección tangencial al hilo pero perpendicular al plano del papel? Justificar.
Datos:
- Constante dieléctrica en el vacío, $\varepsilon_0 = 8,854 \times 10^{-12} ~ C^2/(N m^2)$
- $\sigma=10 ~ \mu C / m^2$
- $L = 20 ~ cm$
- $m=50 ~ g$
- $q = 10 ~ \mu C$
- $g=9.8 ~ m/s^2$
Resolución
Por cuestiones de tiempo no he trabajo todavía en este problema. Si quisieras que dedique mi tiempo a seguir escribiendo resoluciones a problemas como este, ayudame con un aporte libre y voluntario. El tiempo que me lleva preparar y escribir cada resolución excede el que puedo usar en mis tiempos libres.