N°03-2021

Enunciado

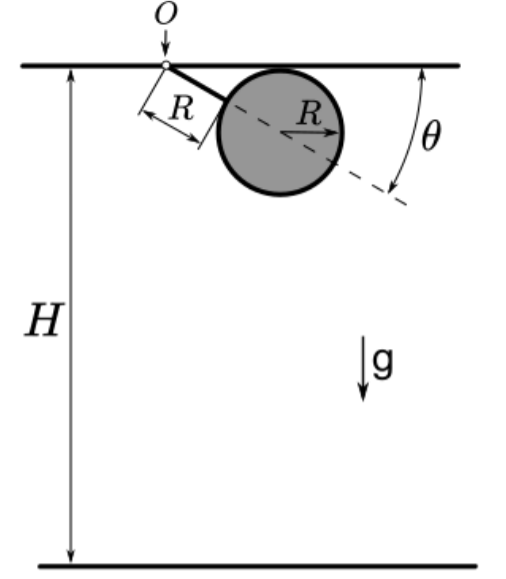
Un disco homogéneo de masa $M$ y radio $R$ está unido rígidamente al extremo de una varilla de largo $R$ y masa despreciable. El otro extremo de la varilla está sujeto al techo de manera que el sistema disco-varilla puede girar libremente alrededor del punto $O$, bajo la acción de la gravedad. Se denomina $\theta$ al ángulo que forma la varilla con el techo.

El sistema se encuentra en reposo cuando el disco está en contacto con el techo en la posición que se indica en la figura. A tiempo $t=0$ el disco se despega del techo, y el sistema disco-varilla rota al rededor del punto $O$ como un cuerpo rígido hasta alcanzar la posición $\theta=\pi/2$. En ese momento ($t=t_1$), el disco se separa de la varilla y continúa con su movimiento como cuerpo libre hasta alcanzar el suelo en $t=t_2$. La distancia desde el suelo hasta el techo es $H=10R$.

Dato: el momento de inercia del disco respecto del centro de masa es $I_{cm} = \frac{1}{2}MR^2$

a) Determine la velocidad del centro de masa del sistema disco varilla en $t_1$

b) Calcule $t_2-t_1$ e indique la posición del disco al alcanzar el suelo

c) Cuantas vueltas da el disco entre $t_1$ y $t_2$

Resolución

a)

Antes que nada, hagamos un balance energético. Si elegimos el punto $O$ como origen de coordenadas, el sistema tiene inicialmente una energía potencial $U_0=-MgR$. Al tiempo $t_1$ el sistema tendrá una energía potencial $U=-2MgR$ y una energía cinética $T$ (sobre la cuál veremos dos formas de determinación). Como no existen fuerzas no conservativas que hagan trabajo, se conserva la energía mecánica $E=T+U$ y por lo tanto,

$$ U_0 = T + U \Rightarrow T=MgR. ~~~~~~~ (1) $$

La energía cinética puede expresarse de las siguientes dos formas:

$$ \begin{cases} \begin{split} T&= \frac{1}{2}M v_{cm}^2+ \frac{1}{2}I_{cm} \omega^2; ~~~~~~~ (2) \\ T&=\frac{1}{2}I_{O} \omega^2. ~~~~~~~~~~~~~~~~~~~~~~~~~~~~ (3) \end{split} \end{cases} $$

Donde $v_{cm}$ es la velocidad del centro de masa del sistema (que coincide con el centro de masa del disco, ya que la varilla es imponderable), $\omega$ es la velocidad angular y $I_O$ es el momento de inercia respecto del eje de giro que pasa por el punto $O$.

Para desarrollar la relación (2) se debe tener en cuenta que el punto $O$ se encuentra en reposo y por lo tanto, por la condición de rodadura, las velocidades están relacionadas mediante la igualdad $v_{cm}=2R\omega$. Para desarrollar (3) hay que tener en cuenta, además, el Teorema de Steiner que vincula los momentos de inercia de la forma $I_O= I_{cm}+M(2R)^2$. No es difícil demostrar que por ambos caminos se obtiene el siguiente resultado:

$$ T=\frac{9}{16}M v_{cm}^2. $$

Finalmente, utilizando en (1) y despejando, obtenemos que

$$ \boxed{v_{cm} = \frac{4}{3} \sqrt{gR}}. ~~~~~~~ (4) $$

b)

A partir de $t_1$ el cuerpo inicia un movimiento de traslación de tipo parabólico. Como el techo se encuentra a una altura $H=10 R$, en el instante $t_1$ el centro de masa se encuentra a una altura $y_1=8R$. En el instante $t_2$, que es cuando hace contacto con el suelo, el centro de masa se encuentra a una altura $y_2=R$. Tomando como origen de coordenadas el punto $O’$ (Figura A), ubicado en el suelo a la misma vertical que $O$, las ecuaciones horarias del centro de masas son:

$$ \begin{cases} \begin{split} y_2&=y_1-\frac{1}{2}g (\Delta t)^2 ~~~~~~~ (5) \\ x_2&=-v_{cm} \Delta t ~~~~~~~~~~~~~~~~~ (6) \end{split} \end{cases} $$

Donde $\delta t=t_2-t_1$. De (5) resulta que

$$ \boxed{\Delta t=\sqrt{\frac{14R}{g}} }. ~~~~~~~ (7) $$

Así, remplazando (4) y (7) en (6), obtenemos la coordenada horizontal

$$ x_2=-\frac{4\sqrt{14}}{3} R. ~~~~~~~ (8) $$

Así, la posición del centro de masa en el instante $t_2$ es

$$ (x_2,y_2) = \left( -\frac{4\sqrt{14}}{3} R, R \right) $$

c)

Durante el intervalo de tiempo $\Delta t$ el disco ha girado un águlo dado por $\Delta \phi = \omega \Delta t = \frac{v_{cm}}{2R} \Delta t$, que por (4) y (7) puede expresarse como

$$ \Delta \phi = \frac{2\sqrt{14}}{3} $$

y la cantidad de vueltas es

$$ \boxed{n =\frac{\Delta \phi}{2 \pi} = \frac{\sqrt{14}}{3\pi}}. $$

$$ \boxed{\text{FIN}} $$