N°02-2021
Enunciado
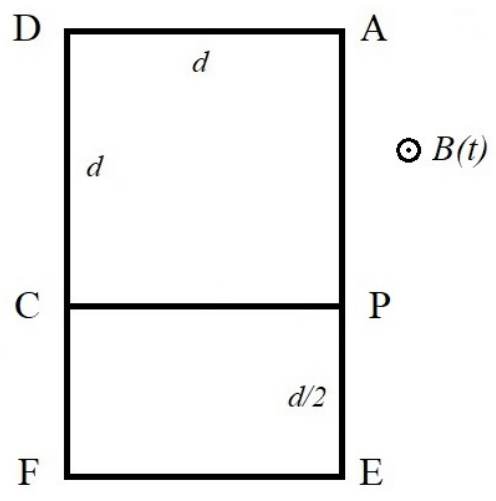
El circuito de la figura anterior está formado por alambres con una resistencia por unidad de longitud $r ~ [\Omega/m]$. Las longitudes de los elementos del circuito son $d$ y $d/2$, según se indica en la figura. El circuito se encuentra inmerso en un campo magnético homogéneo, cuya intensidad cambia con el tiempo según $B(t)=kt$, con $t \geq 0$
a) Despreciando los efectos de autoinducción, calcule las corrientes que circulan en cada rama del circuito.
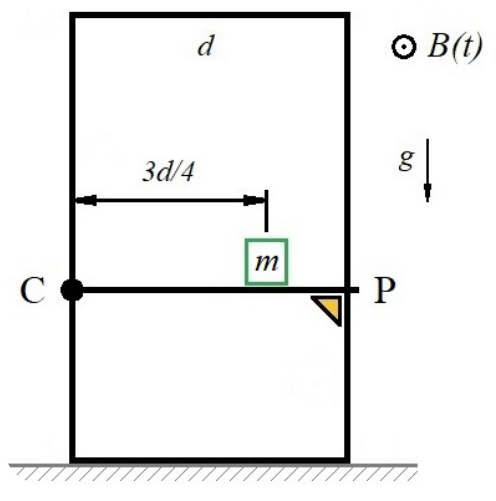
Suponga ahora que la rama del circuito se encuentra apoyada sobre una mesa. El punto $C$ es articulado y el punto $P$ puede deslizar, manteniendo todo el tiempo la continuidad eléctrica, pero posee un tope que previene la caída de la barra $CP$ (de masa despreciable). Una pesa de masa $m$ se coloca en la barra tal como indica la segunda figura. Todo el sistema se encuentra bajo la acción de la gravedad.
b) ¿Para qué valor del tiempo $t$ la reacción en el soporte $P$ se anula?
Resolución
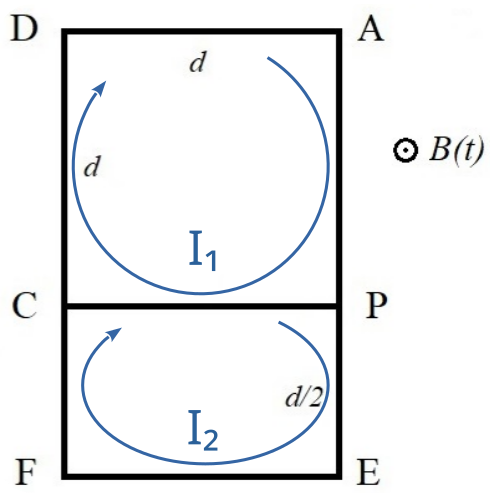
Figura A
Representación de la circulación de las corrientes inducidas en cada rama.
a)
Aplicaremos el método de mallas para determinar las corrientes en cada una de las dos mallas que conforman el circuito (Figura A). El balance energético en ellas está dado por el siguiente sistema de ecuaciones:
$$ \begin{cases} \begin{split} \mathcal{E}_1 = 3drI_1 + dr I_{CP} \\ \mathcal{E}_2 = 2drI_2 - dr I_{CP} \end{split} \end{cases} $$
donde $\mathcal{E}_i$ es la f.e.m. inducida en la i-ésima malla y $I_{CP} = I_1-I_2$ es la corriente en la rama $CP$. Podemos maquillar el sistema de ecuaciones para convertirlo en
$$ \begin{cases} \begin{split} \frac{\mathcal{E}_1}{3dr} = I_1 + \frac{I_{CP}}{3} ~~~~~~ (1) \\ \frac{\mathcal{E}_2}{2dr} = I_2 - \frac{I_{CP}}{2} ~~~~~~ (2) \end{split} \end{cases} $$
y restando la segunda a la primera
$$ \begin{split} \frac{\mathcal{E}_1}{3dr} -\frac{\mathcal{E}_2}{2dr} = I_1 - I_2 + \frac{I_{CP}}{3} + \frac{I_{PC}}{2} \\ \frac{\mathcal{E}_1}{3dr} -\frac{\mathcal{E}_2}{2dr} = I_{CP} + \frac{I_{CP}}{3} + \frac{I_{CP}}{2}, \end{split} $$
de donde resulta que
$$ I_{CP} =\frac{2\mathcal{E}_1 - 3\mathcal{E}_2}{11dr} ~~~~~~ (3). $$
Por otro lado, la f.e.m. inducida en la i-ésima malla de area $S_i$ está determinada por la Ley de Faraday-Lenz:
$$ \mathcal{E}_i= - \frac{d \Phi_i}{dt} $$
donde el flujo magnético $\Phi_i$ está dado por
$$ \Phi_i= \int_{\mathcal{S}_i} \bar{B}\cdot d \bar{S} = B(t) S_i = kt S_i, $$
de manera que
$$ \mathcal{E}_i= - k S_i. $$
Teniendo en cuenta que $S_1 = d^2$ y $S_2 = d^2/2$
$$ \begin{cases} \begin{split} &\mathcal{E}_1= - kd^2 ~~~~~~~ (4)\\ &\mathcal{E}_2= - kd^2/2 ~~~~~~ (5) \end{split} \end{cases} $$
Remplazando (4) y (5) en (3)
$$ I_{CP} = -\frac{k d}{22r}. ~~~~~~ (6) $$
Y remplazando (4), (5) y (6) en el sistema (1)-(2) obtenemos que
$$ \boxed{ \begin{cases} \begin{split} I_1&=-\frac{7k d}{22r} \\ I_2&=-\frac{3k d}{11r}, \end{split} \end{cases} } $$
donde el signo negativo indica que las corrientes circulan en un sentido horario y a partir de ese hecho podemos interpretar que el signo negativo en (6) indica que la corriente en la rama $CP$ circula en el sentido $P \to C$.
b)
La fuerza sobre un elemento de corriente $ I_{CP } d \overline{l}$ del tramo $CP$, debida a la presencia del campo magnético es: $$ d \bar{F}_B=I_{CP} ~ d \overline{l} \times \bar{B} $$
Por las direcciones de la corriente y el campo magnético, se observa que dicha fuerza tiene una dirección vertical hacia arriba cuyo módulo es $$ d F_B=|I_{CP}| B \ dl . ~~~~~~~ (7) $$
Cuando el elemento de corriente $ I_{CP} d \overline{l}$ se encuentra en la posición $\overline{l}$ respecto del punto $C$, genera un torque
$$ d \overline{\tau}_B= \overline{l} \times d \bar{F}_B $$
que en valor absoluto puede escribirse como
$$ d \tau_B= l \ d F_B ~~~~~~~ (8) $$
Así, por (6), (7) y (8), tendremos que:
$$ \begin{split} \tau_B &= \int_{0}^{d} l \ d F_B \\ &=\left| I_{CP} \right| B(t) \int_{0}^{d} l d l \\ &=\left| I_{CP} \right| (kt) \frac{d^2}{2} \\ &=\frac{k^2 d^3}{44r} t ~~~~~~~ (9) \end{split} $$
Cuando haya transcurrido un tiempo $\mathcal{T}$ tal que el valor de este torque se compense con el generado por la fuerza normal ejercida por la pesa sobre la barra $CP$, la barra comenzará a levantarse y se anulará la fuerza normal creada por el soporte $P$. Es decir, debe cumplirse: $$ \tau_B \left( \mathcal{T} \right)=\frac{3}{4}dmg $$ por lo que, junto con (9), podemos deducir lo siguiente $$ \boxed{\mathcal{T} = \frac{33mgr}{k^2d^2}}. $$