N°01-2021

Enunciado

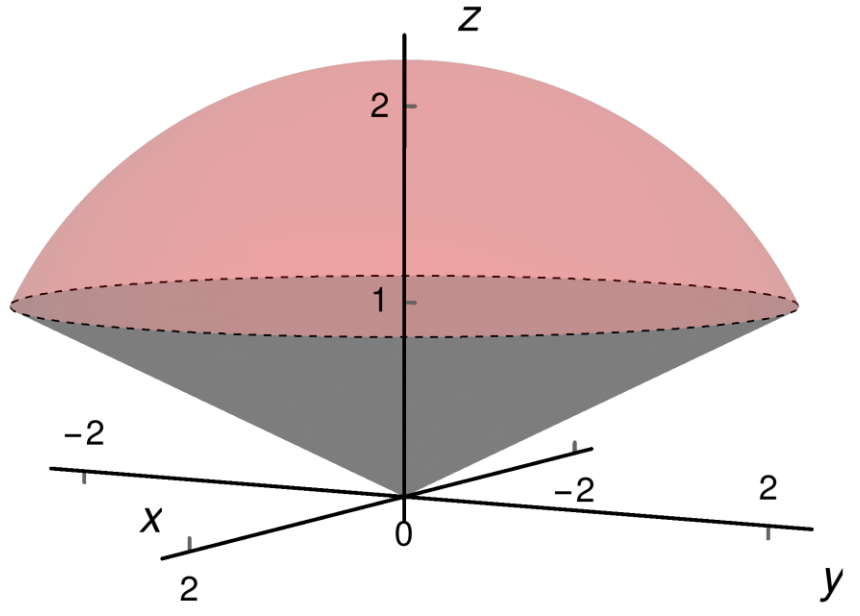
Considere el sólido $W$ encerrado por el cono $x^2 + y^2 =4z^2 $ y la esfera $x^2 + y^2 + z^2 = 5$, siendo $z \geq 0$. Sea $\partial W$ la frontera de $W$ orientada con la normal exterior y $\vec{F}: \mathbb{R}^3 \rightarrow \mathbb{R}^3$ el campo vectorial dado por $\vec{F}(x,y,z) = (y^2,xy,xz)$.

a) Calcular $\text{vol}(W)$ (el volumen de $W$).

b) Mostrar que el máximo valor que alcanza la función $\text{div}( \vec{F})$ en $W$ es 4.

c) Probar que $\left|\int_{\partial W} \vec{F} \cdot d\vec{S}\right| \leq 4 \text{vol}(W)$.

d) Sea $S = { (x,y,z) : x^2 + y^2 + z^2 = 5 , z \geq 1 } $ el casquete esférico superior de $\partial W$ (orientado con la misma normal que $\partial W$). Calcular $\int_S \text{rot}( \vec{F} ) \cdot d \vec{S}$.

Resolución

a)

Dado que el volumen $W$ está constituido por un cono cerrado por una esfera centrada en el origen, escribimos las ecuaciones que definen las superficies en coordenadas esféricas:

$$ \begin{split} &\text{(Esfera)} \ \ r^2 = 5; \\ &\text{(Cono)} \ \ cos( \theta) = 1/ \sqrt{5}. \end{split} $$ Entonces, utilizando estas como límites podemos calcular la integral de volumen:

$$ \begin{split} \text{vol}(W) &= \iiint_W dV \\ &= \iiint_W r^2 sen( \theta ) dr d \phi d \theta \\ &= \int_0^{2\pi} d\phi \int_0^{arccos(1/ \sqrt{5})} d\theta ~ sen( \theta ) \int_0^{\sqrt{5}}dr ~ r^2 \end{split} $$

es decir,

$$ \boxed{\text{vol}(W) = \frac{10 \pi}{3} \left( \sqrt{5} - 1\right) }. $$

b)

La divergencia de $\vec{F}(x,y,z) = (y^2,xy,xz)$ está dada por $$ \nabla \cdot \vec{F} = 2x, $$

y como $\nabla(\nabla \cdot \vec{F}) = (2,0,0) \neq \vec{0}$, la divergencia no cuenta con extremos relativos, de manera que el valor máximo en $W$ corresponderá al valor máximo que puede adquirir la variable $x$ dentro del mismo. Tal valor es $x_{\text{máx}}=2$ y por lo tanto

$$ \boxed{\left( \nabla \cdot \vec{F} \right)_{\text{max}} = 2x_{\text{max}} = 4 }. ~~~~~~~~~~~~(1) $$

c)

Podemos aplicar, sucesivamente, el Teorema de la Divergencia de Gauss, la desigualdad triangular y la relación (1) para obtener:

$$ \begin{split} \left|\int_{\partial W} \vec{F} \cdot d\vec{S}\right| &= \left|\int_{W} \nabla \cdot \vec{F} dV \right| \\ &\leq \int_{W}\left|\ \nabla \cdot \vec{F} \right| dV \\ &\leq \int_{W}\left( \nabla \cdot \vec{F} \right)_{max} dV = 4 \int_{ W} dV \end{split} $$

es decir,

$$ \boxed{\left|\int_{\partial W} \vec{F} \cdot d\vec{S}\right| \leq 4 \text{vol}(W)}. $$

d)

Sea $\partial S = \lbrace (x,y,z) : \ x^2+y^2=4, \ z=1 \rbrace$ la frontera de $S$, entonces, por el Teorema de Stokes

$$ \int_S \text{rot}( \vec{F} ) \cdot d \vec{S} = \oint_{\partial S} \vec{F} \cdot d \vec{r}. $$

Como $d \left. \vec{r} \right|_{\partial S} = (-dx,dy,0)$, tendremos que

$$ \int_S \text{rot}( \vec{F} ) \cdot d \vec{S} = \oint_{\partial S} \left( -y^2 dx + xy dy \right). $$

Por otro lado, si aplicamos el Teorema de Green para la superficie $S’ = \lbrace (x,y,z) : x^2 + y^2 \leq 4 , \ z = 1 \rbrace $ entonces

$$ \oint_{\partial S} \left( -y^2 dx + xy dy \right) = \int_{S’} 2y dx dy, $$

y por lo tanto,

$$ \int_S \text{rot}( \vec{F} ) \cdot d \vec{S} = \int_{S’} 2y dx dy. $$ Para desarrollar al integral del miembro derecho es necesario parametrizar las coordenadas cartesianas en términos de coordenadas polares (en el plano $z=1$), es decir,

$$ \begin{cases} \begin{split} &x = \rho\cos \varphi \\ &y = \rho \sin \varphi \\ &0 \leq \rho \leq 2, \ 0 \leq \varphi < 2 \pi, \end{split} \end{cases} $$

y por lo tanto, teniendo en cuenta el jacobiano $\frac{\partial (x,y)}{\partial (\rho,\varphi)} = \rho$:

$$ \int_S \text{rot}( \vec{F} ) \cdot d \vec{S} = \int_{S’} 2y dx dy = \int_{0}^{2 \pi} d \varphi \int_{0}^{2}d \rho \ 2 \rho^2 \sin \varphi $$

Como $\int_{0}^{2 \pi} d \varphi \sin \varphi = 0$, entonces

$$ \boxed{\int_S \text{rot}( \vec{F} ) \cdot d \vec{S} = 0}. $$