Mecánica N°02-2020

Enunciado

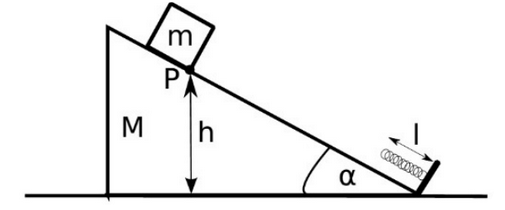
Un bloque de masa $m$ se encuentra en reposo sobre una cuña de masa $M$ que está apoyada sobre una superficie horizontal como se muestra en la figura. Todas las superficies carecen de fricción. La cuña además tiene anexada en su parte inferior un resorte de longitud $l$, constante elástica $k$ y masa despreciable.

a) Si el sistema parte del reposo estando el punto $P$ del bloque a una distancia $h$ sobre la superficie horizontal, determine la velocidad de la cuña en el instante en que el bloque toca el resorte.

b) Calcule la máxima longitud de compresión del resorte.

Resolución

a)

1) La conservación de la energía mecánica del sistema

Un análisis energético nos puede ser de gran utilidad para determinar la velocidad de la cuña en el momento en que el bloque toca el resorte. Como no existen fuerzas disipativas, recurriremos a la conservación de la energía mecánica del sistema. Para ello, ¡no hay que descuidar el hecho de que la cuña se mueve! En la Figura A están representados los estados inicial y final. Al principio los cuerpos están en reposo y, si elegimos como referencia el suelo, el sistema sólo tiene una energía potencial $mgh$. Luego, cuando $m$ llega al resorte, éste disminuye su energía potencial a un valor $mg l \sin \alpha$, lo cual se traduce en un aumento de las energías cinéticas de los cuerpos, que adquieren velocidades que denominaremos $v_m$ y $v_m$, respectivamente. Podemos expresar el balance energético a traves de la siguiente igualdad

$$ mgh = mgl \sin \alpha + \frac{1}{2} m v_m^2+ \frac{1}{2} M v_M^2. $$

Antes de continuar, maquillemos la relación definiendo $\gamma = \frac{M}{m}$ y juntando todos los términos potenciales:

$$ 2 g \left( h - l \sin \alpha \right) = v_m^2+ \gamma v_M^2 ~~~~~~ (0) $$

En términos de los parámetros conocidos del problema, sólo nos estaría faltando saber cómo es la relación entre la velocidad del bloque $v_m$ y la velocidad de la cuña $v_M$. Para encontrarla nos vamos a nutrir de otros dos aspectos fundamentales: la conservación de la componente horizontal de la cantidad de movimiento y la geometría subyacente a los vínculos.

2) La conservación de la componente horizontal de la cantidad de movimiento del sistema

Como la suma de las fuerzas externas al sistema mecánico no tiene componentes en la dirección horizontal, entonces la componente horizontal de la cantidad de movimiento en esa dirección se conserva¹. Además, como inicialmente las partes del sistema están en reposo, su centro de masa también lo está. La mezcla de esos dos hechos implica que la posición del centro de masa será invariable. Como

$$ x_{CM} = \frac{mx_m+M x_M}{m+M}, $$ entonces $$ x_m = - \frac{M}{m} x_M. $$ O cualquiera de sus derivados $$ dx_m = - \frac{M}{m} dx_M ~~~~~~ (1) $$ $$ v_{mx} = - \frac{M}{m} v_M~~~~~~ (2) $$ Con esta última relación, logramos vincular la velocidad de la cuña con una de las componentes de la velocidad del bloque. Nos queda la mitad del trabajo.

3) La geometría subyacente a los vínculos

La Figura A representa dos fotos, pero en ellas no estamos representado el desplazamiento de los cuerpos sino sólo los estados. La forma en que se muevan los cuerpos estará condicionado por aspectos cinemáticos que son eminentemente geométricos. En este caso, el sólo hecho de que el bloque no se despega de la cuña impone una condición geométrica que impacta en los aspectos cinemáticos. Analicemos la Figura B, donde está representada una configuración del sistema en un instante determinado y la configuración en un instante infinitesimalmente posterior. Se representa el hecho de que la cuña se desplaza en una dirección horizontal una distancia $|dx_M|$ y que el bloque lo hace en $|dx_m|$ en sentido opuesto. A su vez, el bloque disminuye su altura en $|dy_m|$. Dichas distancias están vinculadas geométricamente mediante el triángulo rectángulo de ángulo $\alpha$ que tiene como catetos opuesto y adyacente a $|dy_m|$ y $|dx_m|+|dx_M|$, respectivamente. Usemos la función tangente para vincular los catetos

$$ |dy_m|=(|dx_m|+|dx_M|) \tan \alpha $$

y usemos la relación (1) para modificarla,

$$ |dy_m|=\left( \frac{M}{m}+1 \right) |dx_M| \tan \alpha. $$

De esta forma, como los desplazamientos suceden en los mismos intervalos de tiempo, las velocidades se relacionan de igual forma

$$ |v_{my}|=\left( \gamma+1 \right) |v_M| \tan \alpha ~~~~~~ (3) $$

donde hemos aprovechado que $\gamma = \frac{M}{m}$.

Ahora podemos conjugar lo obtenido en las relaciones (2) y (3). Como $v_m^2 =v_{mx}^2+v_{my}^2$ podemos obtener que: $$ v_m^2 = \left[ \gamma^2 +(1+\gamma)^2 \tan^2 \alpha\right] v_M^2. ~~~~~~ (4) $$

Finalmente, llegó el momento de regresar a la relación (0). Veamos como se combina con (4): $$ \begin{split} 2 g \left( h - l \sin \alpha \right) &= \left[ \gamma^2 +(1+\gamma)^2 \tan^2 \alpha \right] v_M^2+ \gamma v_M^2 \\ 2 g \left( h - l \sin \alpha \right) &= \left[ \gamma^2 +(1+\gamma)^2 \tan^2 \alpha + \gamma\right] v_M^2, \end{split} $$ es decir,

$$ v_M^2= \frac{2 g \left( h - l \sin \alpha \right)}{\left[ \gamma^2 +(1+\gamma)^2 \tan^2 \alpha + \gamma\right]} $$

Y así obtenemos lo pedido. Podemos conformarnos con este resultado, pero es posible factorizar el denominador, para ello hay que considerar el siguiente desarrollo $$ \begin{split} \gamma^2 +(1+\gamma)^2 \tan^2 \alpha + \gamma &= \ \gamma(\gamma+1) +(1+\gamma)^2 \tan^2 \alpha\\ &= (\gamma+1) \left[ \gamma +(1+\gamma) \tan^2 \alpha \right] \\ &= (\gamma+1) \left[ \gamma (1+\tan^2 \alpha) + \tan^2 \alpha \right] \\ &= (\gamma+1) \left[ \frac{\gamma} {\cos^2 \alpha} + \tan^2 \alpha \right] \\ &= \frac{(\gamma+1)(\gamma+\sin^2 \alpha)}{\cos^2 \alpha} \end{split} $$

donde use el hecho de que $1+\tan^2 \alpha = \frac{\cos^2 \alpha+\sin^2 \alpha}{\cos^2 \alpha}= \frac{1}{\cos^2 \alpha}$. Así, la velocidad buscada queda expresada como

$$ \boxed{v_M= \sqrt{\frac{2 g \left( h - l \sin \alpha \right) \cos^2 \alpha}{(\gamma+1)(\gamma+\sin^2 \alpha)}}}. $$

b)

Para determinar la compresión del resorte, podemos recurrir a la conservación de la energía mecánica. La energía potencial gravitatoria que el sistema tiene inicialmente $U_0$ se distribuye en las energías cinéticas $T_m$ y $T_M$ que los cuerpos adquieren, en la energía potencial del resorte $U_k$ y algo de ella permanece en forma de energía potencial gravitatoria $U_f$:

$$ U_0 = T_m + T_M + U_k + U_f $$

La compresión máxima del resorte corresponde al valor máximo de su energía potencial $U_k$, la cual será máxima cuando las energías cinéticas $T_m$ y $T_M$ sean mínimas. Por ello, se debe cumplir que $T_m=T_M=0$, lo cual implica que los cuerpos se detienen al mismo tiempo. En ese caso tendremos que

$$ U_0 = U_{k-\text{máx}} + U_f $$

Para desarrollar esta expresión tengamos en cuenta la Figura C donde representamos los estados inicial y final, respectivamente. En el primero,se tiene energía potencial gravitatoria $U_0mgh$. En el segundo, el resorte adquiere una energía potencial por su compresión máxima en $\delta x$ y la energía potencial disminuye a $mg (l -\delta x) \sin \alpha$, es decir:

$$ mgh = \frac{1}{2} k (\delta x)^2 + mg (l -\delta x) \sin \alpha . $$

Este balance nos lleva a una ecuación cuadrática en $\delta x$

$$ \frac{1}{2} (\delta x)^2- \frac{mg}{k} \sin \alpha ~ \delta x - \frac{mg}{k} (h -l \sin \alpha) = 0, $$ cuyas soluciones son $$ \delta x_{1,2} = \frac{mg}{k} \sin \alpha \pm \sqrt{\frac{m^2g^2}{k^2} \sin^2 \alpha +2 \frac{mg}{k} (h -l \sin \alpha)} $$ y de las cuales sólo la positiva corresponde a la comprensión del resorte $$ \boxed{\delta x = \frac{mg}{k} \sin \alpha + \sqrt{\frac{m^2g^2}{k^2} \sin^2 \alpha +2 \frac{mg}{k} (h -l \sin \alpha)}}. $$