N°12-2018
Enunciado
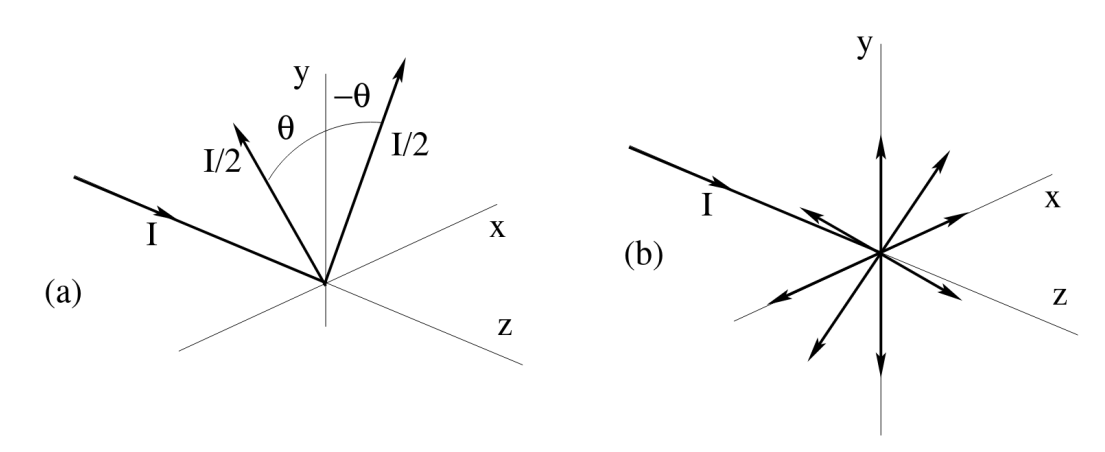
La corriente que circula por un cable recto (en la dirección $z$) se divide en dos partes iguales al llegar a $z = 0$, como se indica en la figura (a). Los dos cables salientes están en el plano $(x, y)$, formando ángulos $\theta$ y $-\theta$ con respecto al eje $y$.
Muestre que en todo punto del plano $(y, z)$ el campo magnético apunta en la dirección $x$.
En el caso de la figura (b) la corriente que llega a $z = 0$ se distribuye uniformemente en el plano $(x, y)$. Generalizando el resultado del punto anterior, pruebe que en este caso el campo magnético en cualquier punto $\overline{r}$ del espacio tiene la dirección del producto vectorial $\overline{r} \times \hat{z}$, y calcule su módulo.
Resolución
A partir de un intercabio con Livio Leiva, egresado del IB, me anime a plantear una propuesta de resolución de este problema. Cuando las propuestas surgen de intercambios suelen ser más nutritivas para quien las escribe. Ojalá lo sean también para quienes en un futuro lean las siguientes líneas.
Para desarrollar la resolución recordaremos la expresión del campo magnético en el punto $\overline{r}$ generado por un elemento de corriente $I d \overline{r}’$ ubicado en el punto $\overline{r}’$:
$$ d \bar{B} (\overline{r}) = \frac{\mu_0}{4 \pi} \frac{I d \overline{r}’ \times (\overline{r}-\overline{r}’)}{||\overline{r}-\overline{r}’||^3} $$
conocida como ley de Biot-Savart.
Tratando de dar respuesta a lo pedido, nos concentraremos exclusivamente en la información direccional que nos brinda la ley de Biot-Savart. Podriamos decir que la misma se encuentra reducida al producto vectorial $d \overline{r}’ \times (\overline{r}-\overline{r}’)$.
Usemos como origen de coordenadas el ya impuesto por el enunciado. Se puede ver que en todos los cables del problema se cumple que el producto $d \overline{r}’ \times \overline{r}’ = \overline{0}$. Entonces, la información direccional se concentra en el producto $d \overline{r}’ \times \overline{r}$.
Por otro lado, los elementos $d \overline{r}’$ tienen la dirección de la corriente, y como nos interesa solo su dirección, podemos introducir el versor $\hat{I}_i$ que determina la dirección de la corriente del i-ésimo cable y tal que $d \overline{r}’_i = ||d \overline{r}’_i||\hat{I}_i $. Así, dado un punto $\overline{r}$, la dirección del campo magnético generado por el i-ésimo cable estará dada por el producto vectorial $\hat{I}_i \times \overline{r}$.
1.
Denominaremos $$ \begin{cases} \hat{I}_0 &= \hat{z}=(0,0,1), \\ \hat{I}_1 &= (\sin \theta,\cos \theta,0), \\ \hat{I}_2 &= (-\sin \theta,\cos \theta,0) \end{cases} $$
a los versores que determinan las direcciones de las corrientes de cada uno de los cables (dejo al lector el trabajo de identificar a cuál cable corresponde cada una de ellas).
Si el punto en cuestión se encuentra en el plano $YZ$, es decir, $\overline{r}=(0,y,z)$, podemos sacar inmediatamente las siguientes conclusiones.
- El campo magnético generado por el cable $\hat{I}_0$ apunta en la dirección del eje $X$, ya que $\hat{I}_0\times \overline{r} = (-y,0,0)$.
- Como los campos magnéticos de los cables $1$ y $2$ tienen el mismo módulo, la dirección de su suma (vectorial) estará dada por la suma de los productos vectoriales
$$ \hat{I}_1 \times \overline{r} + \hat{I}_2 \times \overline{r} = \left( \hat{I}_1 +\hat{I}_2 \right) \times \overline{r}. $$
Es fácil ver que la suma $$ \hat{I}_1 +\hat{I}_2 = (0,2 \cos \theta,0), ~~~~~~ (1) $$ apunta en el eje $Y$ y por lo tanto el campo resultante de tales cables apunta en la dirección del eje $X$.
Así, el campo resultante de los tres cables apunta en la dirección del eje $X$.
2.
Cuando la corriente se distribuye por todo el plano, si buscamos determinar la dirección el campo en cualquier punto $\overline{r}$ del espacio, siempre podremos elegir nuesto sistema de coordenadas de manera tal que:
- $\hat{I}_0=\hat{z}$, y que
- el vector $\overline{r}$ se encuentre en el plano $YZ$.
De esta forma, aprovechando lo demostrado en el inciso anterior, podemos pensar a las corrientes distribuidas por el plano como un continuo de «pares de cables» que subtiendan los ángulos $\theta$ y $-\theta$, respecto del eje $Y$ (con $\theta \in \left[0, \pi \right] $). Los campos generados por cada par de cables apuntarán en la direción del eje $X$, es decir, serán perpendiculares a $\overline{r}$ y a $\hat{z}$. O, en otros términos, tendrá la dirección $\hat{z} \times \overline{r}$.
Para determinar el módulo, aprovecharemos la simetría del problema para aplicar la Ley de Ampère para campos magnetostáticos. En una circunferencia $\mathcal{C}$ de radio $R$ alrededor del eje $Z$, por la cual circula el campo con módulo constante y sólo es atravesada por la corriente fuente $I$ para $z\leq 0$ y por ninguna corriente para $z>0$:
$$ \oint_{\mathcal{C}} \bar{B} \cdot d \bar{r} = B ~ 2 \pi R = \begin{cases} \mu_0 I &\text{ si }~~~~ z\leq 0 \\ 0 & \text{ si } ~~~~ z>0 \end{cases} $$
entonces
$$ \boxed{ B = \begin{cases} \frac{\mu_0 I}{2 \pi R} & \text{ si } ~~~~ z\leq 0 \\ 0 & \text{ si } ~~~~ z>0 \end{cases}. } $$