N°12-2018
Enunciado
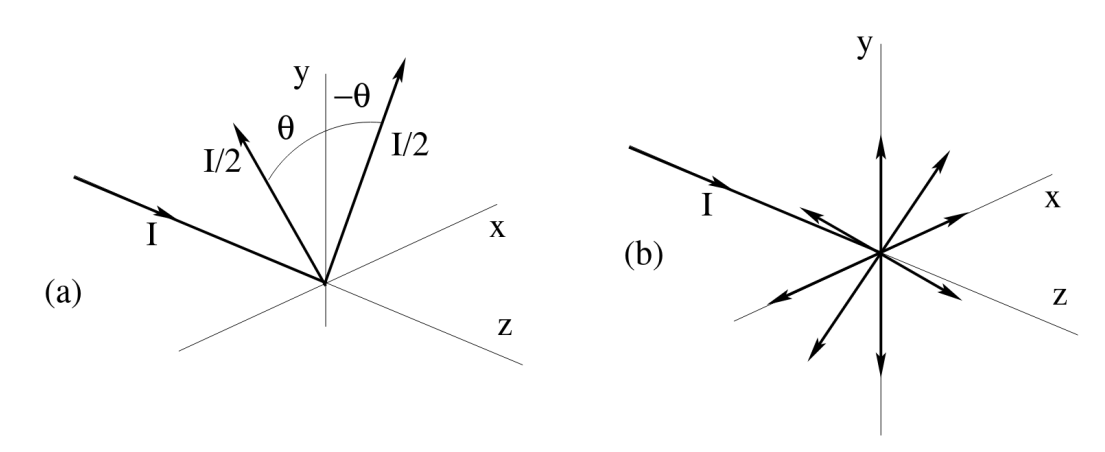
La corriente que circula por un cable recto (en la dirección $z$) se divide en dos partes iguales al llegar a $z = 0$, como se indica en la figura (a). Los dos cables salientes están en el plano $(x, y)$, formando ángulos $\theta$ y $-\theta$ con respecto al eje $y$.
Muestre que en todo punto del plano $(y, z)$ el campo magnético apunta en la dirección $x$.
En el caso de la figura (b) la corriente que llega a $z = 0$ se distribuye uniformemente en el plano $(x, y)$. Generalizando el resultado del punto anterior, pruebe que en este caso el campo magnético en cualquier punto $\overline{r}$ del espacio tiene la dirección del producto vectorial $\overline{r} \times \hat{z}$, y calcule su módulo.
Resolución
1.
Denominaremos $$ \begin{cases} \hat{I}_0 &= \hat{z}=(0,0,1), \\ \hat{I}_1 &= (\sin \theta,\cos \theta,0), \\ \hat{I}_2 &= (-\sin \theta,\cos \theta,0) \end{cases} $$
a los versores que determinan las direcciones de las corrientes de cada uno de los cables. Dado un punto $\overline{r}$, la dirección del campo magnético generado por el i-ésimo cable estará dada por el producto vectorial $\hat{I}_i \times \overline{r}$.
Si el punto en cuestión se encuentra en el plano $YZ$, es decir, $\overline{r}=(0,y,z)$, podemos sacar dos conclusiones inmediatamente:
- el campo magnético generado por el cable $\hat{I}_0$ apunta en la dirección del eje $X$, ya que $\hat{I}_0\times \overline{r} = (-y,0,0)$
- los campos magnéticos de los cables 1 y 2 tienen el mismo módulo, de manera que la dirección de su suma (vectorial) estará dada por la suma de los productos vectoriales $\hat{I}_1 \times \overline{r} + \hat{I}_2 \times \overline{r} = \left( \hat{I}_1 +\hat{I}_2 \right) \times \overline{r}$. Es fácil ver que la suma $$ \hat{I}_1 +\hat{I}_2 = (0,2 \cos \theta,0) ~~~~~~ (1) $$ apunta en el eje $Y$ y por lo tanto el campo resultante de tales cables apunta en la dirección del eje $X$.
Así, el campo resultante de los tres cables apunta en la dirección del eje $X$.
2.
Cuando la corriente se distribuye por todo el plano, si nos interesa el campo en cualquier punto $\overline{r}$ del espacio, siempre podemos elegir nuesto sistema de coordenadas de manera tal que $\hat{I}_0=\hat{z}$ y que el vector $\overline{r}$ se encuentre en el plano $YZ$. Así, aprovechando el ejemplo anterior, podemos pensar a las corrientes distribuidas por el plano como un continuo de «pares de cables» que subtiendan los ángulos $\theta$ y $-\theta$, respecto del eje $Y$. Los campos generados por cada par de cables apuntarán en la direción del eje $X$, es decir, serán perpendiculares a $\overline{r}$ y a $\hat{z}$. O en otros términos, tendrá la dirección $\overline{r} \times \hat{z}$.
Para determinar el módulo, aprovecharemos la simetría del problema para aplicar la Ley de Ampère para campos magnetostáticos. En una circunferencia de radio $R$ alrededor del eje $Z$, por la cual circula el campo con módulo constante y sólo es atravesada por la corriente fuente $I$ para $z\leq 0$ y por ninguna corriente para $z>0$:
$$ \oint_{\mathcal{S}} \bar{B} \cdot d \bar{r} = B ~ 2 \pi R = \begin{cases} \mu_0 I &\text{ si }~~~~ z\leq 0 \\ 0 & \text{ si } ~~~~ z>0 \end{cases} $$
entonces
$$ \boxed{ B = \begin{cases} \frac{\mu_0 I}{2 \pi R} & \text{ si } ~~~~ z\leq 0 \\ 0 & \text{ si } ~~~~ z>0 \end{cases}. } $$