N°03-2017

Enunciado

Calcule la integral: $$ \iint_D \frac{1}{1+x^2+y^2} dx ~dy. $$

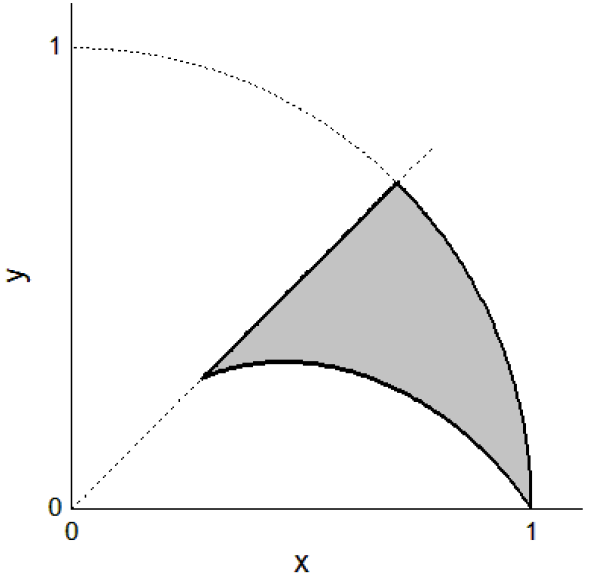
siendo $D$ la región del plano descrita en coordenadas polares por los pares:

$$ \lbrace (r,\theta): \sqrt{2^{1-\theta}-1}\leq r \leq 1, ~ 0 \leq \theta \pi/4\rbrace. $$

Resolución

Si realizamos el cambio de variables a las coordenadas polares, recordando que el jacobiano de la transformación es $r$, tendremos que

$$ \iint_D \frac{1}{1+x^2+y^2} dx ~ dy = \int_0^{\pi/4} \int_{\sqrt{2^{1-\theta}-1}}^1 \frac{r ~ dr ~ d \theta}{1+r^2} $$

Si ahora introducimos la variable $u=1+r^2$:

$$ \begin{split} \iint_D \frac{1}{1+x^2+y^2} dx ~ dy. &= \frac{1}{2}\int_0^{\pi/4} \int_{2^{1-\theta}}^2 \frac{du~d\theta}{u} \\ &= \frac{1}{2}\int_0^{\pi/4} \left[ \ln u \right]_{2^{1-\theta}}^2 ~ d\theta \\ &= \frac{1}{2}\int_0^{\pi/4} \ln 2^{\theta} ~ d\theta \\ &= \frac{\ln 2}{2}\int_0^{\pi/4} \theta ~ d\theta \\ &= \frac{\ln 2}{2} \left. \frac{\theta^2}{2}\right|_0^{\pi/4} \end{split} $$ entonces $$ \boxed{\iint_D \frac{1}{1+x^2+y^2} dx ~dy = \frac{\pi^2 \ln 2}{2^6}}. $$