N°01-2017

Enunciado

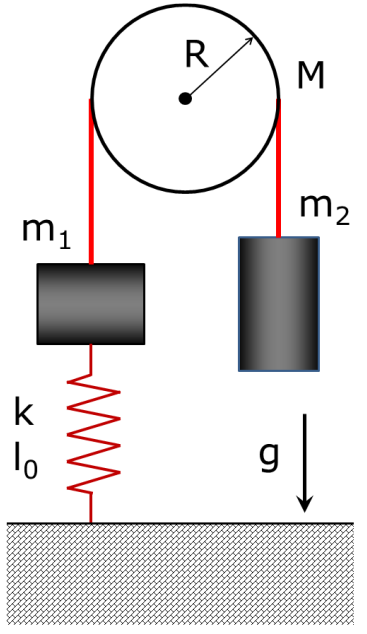
El montaje que se observa en la figura consta de una polea de masa $M$ y radio $R$, una masa $m_1$ a la izquierda, una masa $m_2$ a la derecha, y un resorte de rigidez $k$ y longitud en reposo $l_0$ . La cuerda sin masa que une $m_1$ y $m_2$ no desliza en la polea ni cambia de longitud.

a) Determinar el alargamiento del resorte cuando el sistema está en equilibrio.

A continuación se desplaza ligeramente la masa $m_2$ en dirección vertical desde su posición de equilibrio y se la suelta sin velocidad inicial.

b) Determinar la ecuación que describe el movimiento de la masa $m_2$ .

c) Determinar la frecuencia de las oscilaciones.

Resolución

En el esquema de la Figura A están representadas las fuerzas que actúan sobre las masa $m_1$ y $m_2$. En el segundo caso están presentes la interacción con la tierra, a través del peso $m_2g$, y la interacción con a polea, cuyo medio de interacción es la soga, que se encuentra representada por la fuerza de tensión $T$. En el primer caso, además de tales interacciones está presente la interacción con el suelo, donde el medio de interacción es el resorte y cuya fuerza denominamos $F_k = - k (x-l_0)$. Así, las ecuaciones dinámicas están dadas por:

$$ \begin{cases} \begin{split} T_1 - m_1 g - k (x_1-l_0) &= m_1 ~\ddot{x}_1 \\ T_2 - m_2g &= m_2 ~\ddot{x}_2 \end{split} \end{cases} ~~~~~~ (1) $$

En el caso de la polea, ademas de la fuerza peso y la reacción en su eje, está la interacción con la cuerda. Como existe un rozamiento estático, de rodadura, entre la polea y la cuerda, es importante tener en claro que las tensiones $T_1$ y $T_2$ no tienen por qué ser iguales. En caso de que tal igualdad se cumpla, la misma debe surgir del análisis de las interacciones. En esta oportunidad alcanzará con analizar cómo es que estas fuerzas aportan al torque total sobre la polea respecto de su centro de masas.

En una sección elemental de la soga, para que no haya deslizamiento, es necesario que la tensión $dT$ que genera su interacción con el resto de la soga se compense con la fuerza de rozamiento con la cuerda $df_r$, es decir, $dfr=dT$. Así, el torque elemental de tal fuerza estará dado por $d \tau = R~ df_r= R~dT$, y por lo tanto el torque total será:

$$ \tau = \int d \tau = \int_{T_1}^{T_2} R~dT =R (T_2-T_1) $$

Además $\tau = I \alpha$ con $\alpha$ la aceleración angular e $I$ el momento de inercia de la polea respecto de su centro de masas y por la condición de rodadura $\ddot{x}_1 = - R \alpha$ (consideramos rotaciones positivas en el sentido antihorario, de manera que aumentos en el angulo de rotación produce disminuciones en la posición de la masa $m_1$). Finalmente, como $I= M R^2$

$$ \tau =R (T_2-T_1) = I \alpha = M R^2\alpha = -M R \ddot{x}_1 $$ es decir $$ (T_2-T_1) = -M \ddot{x}_1 ~~~~~~ (2) $$

a) En la posición de equilibrio $x_e$, $T_1=T_2=T$ y las relaciones (1) se reducen a

$$ \begin{cases} \begin{split} T - m_1 g - k (x_e-l_0) &= 0 \\ T - m_2g&= 0 \end{split} \end{cases} $$

que combinándolas permiten deducir que el alargamiento del resorte $\Delta x$ es

$$ \boxed{\Delta x=x_e-l_0=\frac{(m_2-m_1)g}{k}}. $$

b) Fuera del equilibrio las tensiones no coinciden. Para evitar esa dificultad podemos independizarnos de la tensiones mezclando las relaciones (1) y (2) $$ m_2g - m_1 g - k (x_1-l_0) = (m_1+M) ~\ddot{x}_1 -m_2 ~\ddot{x}_2, ~~~~~~ (3) $$

y observar que debemos encontrar la dependencia entre las posiciones $x_1$ y $x_2$, para obtener una ecuación diferencial en $x_2$.

Es posible demostrar que las posiciones están vinculadas a través de un valor constante que depende de la altura del centro de la polea $H$, su radio $R$ y la longitud de la cuerda $L$. Veamos cómo se deduce ese hecho: pensemos que la cuerda está constituida por un tramo $L_1$ que conecta la polea con $m_1$, una cantidad $\pi R$ que rodea la polea y un tramo de longitud $L_2$ que conecta la polea con $m_2$, es decir,

$$ L=L_1+\pi R+L_2 ~~~~~~ (4) $$

A su vez la altura del centro de la polea puede pensarse como dos sumas:

$$ \begin{cases} \begin{split} H&=x_1+L_1 \\ H&=x_2+L_2 \end{split} \end{cases} ~~~~~~ (5) $$

Sumando las relaciones (5) obtenemos $2H=x_1+x_2+L_1+L_2$ y de la relación (4) $L_1+L_2=L-\pi R$, entonces

$$ x_1 = 2H - L +\pi R -x_2, $$

y por lo tanto

$$ \ddot{x}_1 = -\ddot{x}_2 $$

Veamos cómo impactan estos resultados en la relación (3):

$$ \begin{split} m_2g - m_1 g - k (2H - L +\pi R -x_2-l_0) &= - (m_1+m_2+M) ~\ddot{x}_2 \\ (m_2 - m_1) g - k (2H - L +\pi R-l_0) &= - (m_1+m_2+M) ~\ddot{x}_2 - k x_2 \\ -(m_2 - m_1) g+ k (2H - L +\pi R-l_0) &= (m_1+m_2+M) ~\ddot{x}_2 + k x_2 \\ (m_1+m_2+M) ~\ddot{x}_2 + k x_2 &= k (2H - L +\pi R-l_0) -(m_2 - m_1) g \end{split} $$ es decir, $$ \boxed{\ddot{x}_2 + \frac{k}{(m_1+m_2+M)} x_2 = \frac{k (2H - L +\pi R-l_0)}{(m_1+m_2+M)} -\frac{(m_2 - m_1)}{(m_1+m_2+M)} g} ~~~~~~ (6) $$

c) Ya hemos hecho todo el trabajo para determinar la frecuencia de oscilación, aunque hubiese sido más sencillo indentificarla obteniendo la ecuación diferencial para $x_1$. La relación (6) es del tipo $\ddot{x}_2 + \omega^2 x_2 = a $ con $\omega$ la frecuencia de oscilación y $a$ una constante, de manera que

$$ \boxed{\omega = \sqrt{\frac{k}{(m_1+m_2+M)}}}. $$