N°07-2016
Enunciado
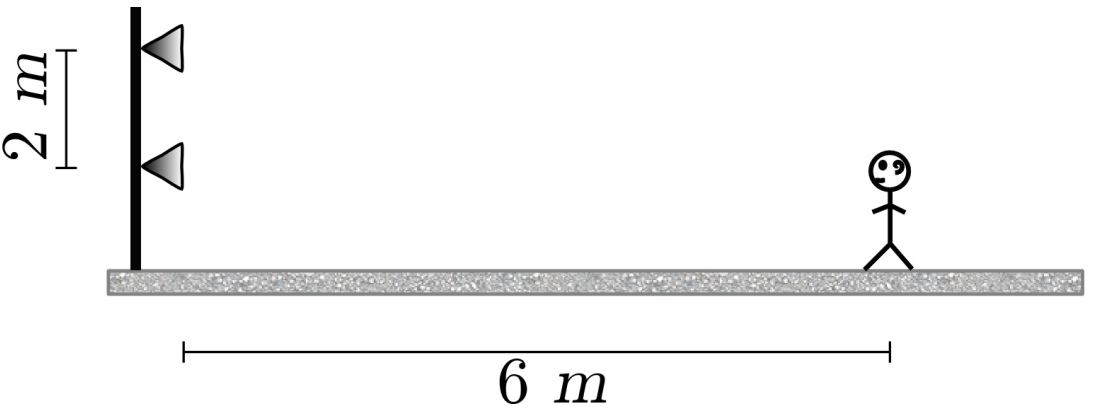
Sobre un poste se han colocado dos altoparlantes, el segundo $2 ~ m$ más alto que el primero. Una persona que está al nivel del primer altoparlante, se encuentra a $6 ~ m$ de distancia de éste. Ambos altoparlantes emiten un sonido de la misma frecuencia y en fase. Considerar que la velocidad del sonido en el aire es de $343~m/s$.
a) ¿Cuál es la frecuencia más baja que el sonido puede tener si la persona percibe un mı́nimo de intensidad en el lugar donde se encuentra parada?
b) Si la frecuencia es la calculada en a), y si la persona avanza lentamente hacia el poste, ¿a qué distancia volverá a percibir un mı́nimo de intensidad?
c) ¿Cuántos mı́nimos de intensidad más percibirá la persona si sigue avanzando hacia el poste?
Nota: En todos los casos, despreciar las variaciones de la intensidad del sonido con la distancia a la fuente.
Resolución
Aunque podemos partir de los resultados teóricos obtenidos en el estudio de la interferencia de ondas, si usualmente no tenemos en claro cuales son las hipótesis que los generan, es recomendable practicar la deducción de los mismos en cada problema.
Consideramos dos fuentes de onda de igual amplitud, frecuencia y fase, representadas por las siguietnes expreisones:
$$ \begin{cases} \begin{aligned} \psi_1 &= \psi_0 \sin (\omega t - kr_1 + \phi), \\ \psi_2 &= \psi_0 \sin (\omega t - kr_2 + \phi). \end{aligned} \end{cases} $$
La onda producida por la superposición estará dada por
$$ \psi = \psi_0 \left[ \sin (\omega t - kr_1 + \phi) + \sin (\omega t - kr_2 + \phi)\right]. $$
Para desarrollarla podemos aprovechar la siguiente identidad trigonométrica, $$ \sin A + \sin B = 2 \cos \left( \frac{A-B}{2} \right) \sin \left( \frac{A+B}{2} \right), $$
de manera que
$$ \psi = 2\psi_0 \cos \left( k\frac{r_2-r_1}{2} \right) \sin \left( \omega t - k\frac{r_1+r_2}{2} + \phi \right) $$
Podemos observar que la amplitud de la onda resultante es
$$ \psi_M = 2\psi_0 \cos \left( k\frac{r_2-r_1}{2} \right). $$
La interferencia es destructiva cuando la amplitud se anula, lo cual es equivalente a pedir que $$ \cos \left( k\frac{r_2-r_1}{2} \right)=0, $$ es decir, debe cumplirse que $$ k\frac{r_2-r_1}{2}=(2n+1)\frac{\pi}{2} \ \text{con } n\in \mathbb{Z}, $$ que simplificando resulta en pedir que
$$ k \Delta r =(2n+1)\pi \ \text{con } n\in \mathbb{Z}. ~~~~~~\text{(1)} $$
a)
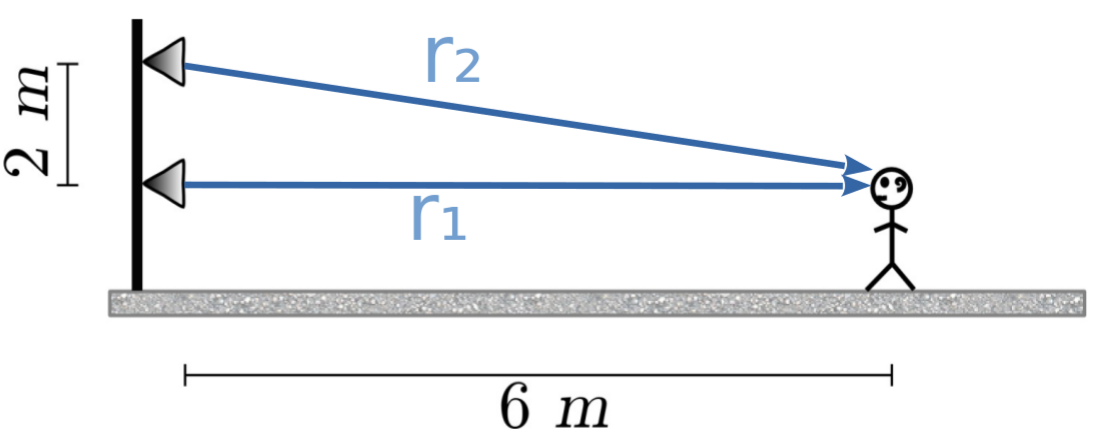
Figura 1
Consideremos la situación de interés: los parlantes son las fuentes y la posición de la cabeza (oídos) de la persona determina el punto del espacio donde nos interesa estudiar la superposición. Podemos identificar las distancias $r_1$ y $r_2$ en el esquema de la Figura 1. Si hacemos uso de la relación $k=\omega/c$, con $c$ la velocidad de propagación, podemos expresar la relación (1) como $$ \omega =(2n+1)\frac{\pi c}{\Delta r} \ \text{con } n\in \mathbb{Z}. $$
Vemos que, cuando $\Delta r$ es positivo, la frecuencia angular mínima corresponde a $n=0$, entonces
$$ \omega_{min} =\frac{\pi c}{\Delta r}. ~~~~~~\text{(2)} $$
Como $r_1=6~ m$ y $r_2=\sqrt{(2~m)^2+r_1^2} = 2\sqrt{10} ~ m$ entonces $\Delta r \approx 0.32 ~ m$ y $\omega_{min} \approx3367,4 ~ s^{-1}$. Por ello, la frecuencia es $\boxed{f_{min} =\omega_{min}/2\pi=536 ~ \text{Hz}}$1.
b)
Si consideramos una configuración diferente a la inicial, podemos expresar la diferencia entre las posiciones con la siguiente notación $\Delta r’ = r_2’-r_1’$. Así, la relación (1) puede expresarse como
$$ \frac{\omega_{min}}{c} \Delta r’ =(2n+1)\pi \ \text{con } n\in \mathbb{Z}, $$ lo cual se puede reescribir, teniendo en cuenta la relación (2), como
$$ \Delta r’ =(2n+1)\Delta r \ \text{con } n\in \mathbb{Z}, $$ donde $\Delta r$ es la diferencia inicial. Para $n=0$ tenemos la configuración inicial, para valores positivos de $n$ tenemos aumentos en la diferencia y para valores negativos tenemos disminuciones. Surge así la necesidad de hacerse la pregunta ¿qué sucede con $\Delta r’$ si $r’_1<r_1$ y $r’_2<r_2$? es decir, ¿qué sucede con la diferencia a medida que las distancias disminuyen?. Es un poco anti intuitivo, pero se puede demostrar2 que dicha diferencia aumenta. Entonces, el siguiente punto de intensidad mínima corresponde a $n=1$, es decir, $\Delta r’=3 \Delta r \approx 0.96~ m$.
Para conocer $r’_1$, podemos aprovechar que $r’_2 = r’_1 + \Delta r’$ y remplazar en el Teorema de Pitagoras aplicado al triángulo en cuestión:
$$ \begin{split} r’^2_2 &= r’^2_1+d^2 \\ \left(r’_1 + \Delta r’ \right)^2 &= r’^2_1+d^2 \\ r’^2_1 + 2 r’_1 \Delta r’ +(\Delta r’)^2&= r’^2_1+d^2 \\ 2 r’_1 \Delta r’+(\Delta r’)^2&= d^2 \\ \end{split} $$
de donde podemos despejar para obtener
$$ r’_1 = \frac{d^2-(\Delta r’)^2}{2\Delta r’} = \frac{(d-\Delta r’)(d+\Delta r’)}{2\Delta r’} $$ que nos lleva a una distancia $\boxed{r’_1 \approx 1.6 ~ \text{m}}$.
c)
El valor máximo de $\Delta r’$ es la distancia $d=2m$ entre los micrófonos, entonces: $$ \Delta r’ =(2n+1)\Delta r \leq d \Rightarrow n \leq \frac{d/\Delta r - 1}{2} $$ es decir, $n \leq 2.625$, lo cual implica que sólo percibirá un mínimo más, además de los dos primeros, es decir, percibirá un total de 3 mínimos.
¿Como son las regiones de intensidad míníma? ¿Qué hay detras del análisis anterior?
Interpretemos en un sentido más general la ecuación (1), que podemos escribir como $$ \Delta r =(2n+1)\frac{c}{2 f} \ \text{con } n\in \mathbb{Z}, ~~~~~~\text{(3)} $$ y vemos para un valor fijo de la frecuencia y la velocidad de propagación, nos dice que el conjunto de puntos del plano (o del espacio) asociados a un valor fijo de $n$ corresponden a aquellos puntos tales que la diferencia $\Delta r$ es constante. Es sabido, que las curvas (superficies) que cumplen con esa característica son las denominadas hipérbolas (hiperboloides) de dos hojas. Es por ello que cada valor de $n$ tiene asociada una hipérbola (hiperboloide) de dos hojas, y por lo tanto la relación (3) constituye una familia infinita de ellas.
En la Simulación 1 se puede observar la formación de la familia de hipérbolas que se observan con un toco oscuro y corresponden a la interferencia destructiva.
En la Simulación 2 se esquematiza la propagación de las ondas si estuviésemos parados en un punto de alguna de las hipérbolas, que corresponden a los canales que se observan.
Simulación 1

Simulación 2
En la afinación temperada la nota $A_4 = 440~\text{Hz}$, de manera que $f_{min}=536~\text{Hz}$ estará entre las notas $C_5=523~\text{Hz}$ y $\text{#}C_5=554~\text{Hz}$ ↩︎
Para ello usaremos el Teorema de Pitágoras en el triángulo rectángulo formado por las distancias $r_1$, $r_2$ y la distancia $d$ entre los micrófonos: $$ \begin{split} r_2^2 &= r_1^2+d^2 \\ r_2^2 - r_1^2&=d^2 \\ (r_2 - r_1)(r_2 + r_1)&=d^2 \\ \Delta r &=\frac{d^2}{(r_2 + r_1)} \\ \end{split} $$ De la última relación vemos fácilmente que al disminuir $r_1$ y $r_2$ la diferencia $\Delta r$ aumenta. ↩︎