N°06-2016
Enunciado
Un avión debe dirigirse desde el punto de coordenadas: latitud $45^{\circ} ~ N$, longitud $0^{\circ} $, hasta el punto: latitud $45^{\circ} ~ N$, longitud $90^{\circ} ~ E$ (recuerde que el ecuador corresponde a $0^{\circ}$ de latitud).
a) ¿Qué distancia recorre si viaja en una ruta de latitud constante?
b) Teniendo en cuenta que la ruta de latitud constante no corresponde al camino más corto, describir cualitativamente cuál serı́a dicho camino y calcular qué distancia recorrerı́a el avión al realizarlo.
c) Para la trayectoria calculada en b), encontrar la máxima latitud alcanzada durante el recorrido.
Nota: Suponer que la Tierra es una esfera perfecta de radio $R = 6370~\text{km}$ y despreciar efectos asociados a variaciones de altura del avión.
Resolución
a)
Con un esquema prolijo podemos reconocer que un movimiento a la latitud contante consiste en un movimiento circular en un plano perpendicular al eje de la tierra (FIgura 1). El radio $r$ de la circunferencia está dado por la latitud y el radio de la tierra, $r=R \cos (45^{\circ}) =R/\sqrt{2}=4504.3~\text{km}$ y el angulo de recorrido por la variación en la longitud, que en este caso es $90^{\circ}=\pi/2$. Así, el recorrido es $\boxed{S_a=\frac{\pi}{2} r =7075.3~\text{km}}$.
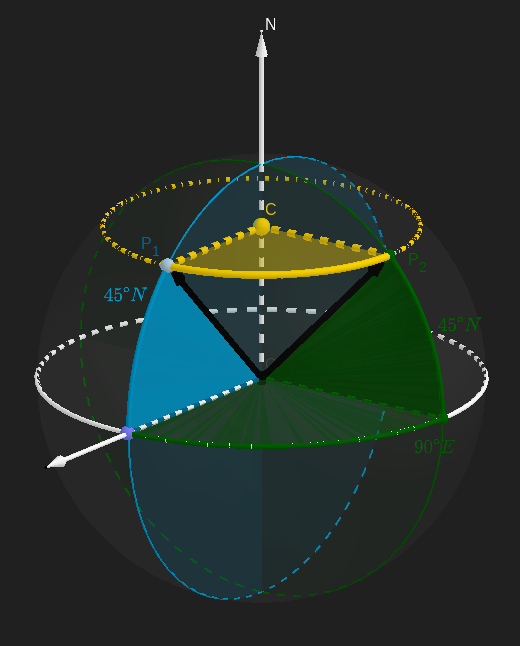
Figura 1
b)
Cuando el movimiento es sobre la superficie de la Tierra y el avión mantiene la dirección de su rumbo, siempre será posible encontrar una circunferencia de radio $R$ que contiene su movimiento (Figura 2). Como las posiciones inicial y final pueden caracterizarse por dos vectores $\overline{R}_1$ y $\overline{R}_2$, respectivamente, podremos encontrar el ángulo de desplazamiento $\theta$ mediante su producto interno:
$$ \cos \theta = \frac{\overline{R}_1 \cdot \overline{R}_2}{||\overline{R}_1||~||\overline{R}_2||}. $$
En un sistema de coordenadas cartesiano $\overline{R}_1=(R/\sqrt{2},0,R/\sqrt{2})$ y $\overline{R}_2=(0,R/\sqrt{2},R/\sqrt{2})$, entonces
$$ \cos \theta = \frac{R/2}{R~R}= \frac{1}{2}, $$
es decir, $\theta = \pi /3 = 60^{\circ}$, y por lo tanto el recorrido es $\boxed{S_b=\frac{\pi}{3} R =6670.6~\text{km}}$.
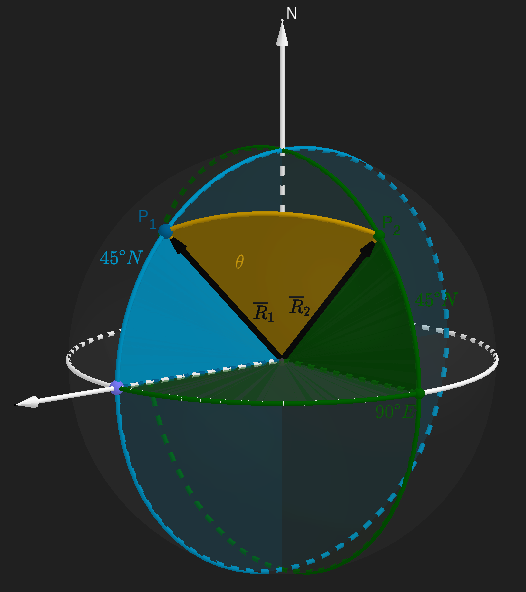
Figura 2
c)
Por simetría, dado que las posiciones inicial y final tienen la misma latitud, la máxima latitud debe darse en la mitad del recorrido. La posición de máxima latitud estará dada por $\overline{R}_{\text{lat. máx}}= R \hat{u}$ donde $\hat{u}$ es un versor en la dirección media entre $\overline{R}_1$ y $\overline{R}_2$. Podemos hallar tal versor normalizando el vector
$$ \overline{R}_1+\overline{R}_2= (\frac{R}{\sqrt{2}},\frac{R}{\sqrt{2}},\sqrt{2} R), $$ cuya norma es $||\overline{R}_1+\overline{R}_2||=\sqrt{3} R$ y por lo tanto
$$ \hat{u}=\frac{\overline{R}_1+\overline{R}_2}{||\overline{R}_1+\overline{R}_2||}= (\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}},\sqrt{\frac{2}{3}} ). $$
El ángulo que subtiende dicho versor con el eje $z$ es el complemento de la latitud máxima $\varphi_{\text{máx}}$. Es decir, por un lado $\gamma + \varphi_{\text{máx}} = \pi/2$ y por el otro $\cos \gamma = \hat{u} \cdot \hat{z}= \sqrt{\frac{2}{3}}$ entonces $\sin \varphi_{\text{máx}} = \cos \gamma= \sqrt{\frac{2}{3}}$. De esta forma obtenemos que $\boxed{\varphi_{\text{máx}}=54.7^{\circ}}$.