N°01-2015
Enunciado
Un disco de material plástico, radio $R$ y espesor despreciable, tiene una carga eléctrica $q$ uniformemente distribuida sobre su superficie. Se hace girar el disco con una frecuencia angular $\omega$ alrededor de su eje. Encontrar el campo de inducción magnética $B$ para puntos situados a lo largo de ese eje.
Resolución
Estrategia de resolución
La carga eléctrica está uniformemente distribuida, es decir, podemos definir una densidad de carga superficial $$ \sigma =\frac{q}{\pi R^{2}}, ~~~~~~\text{(1)} $$ y comenzar a concebir al dico girando como un continuo de espiras de corriente de radio $r \leq R$ (Figura 1). Si somos capaces de encontrar la corriente $dI(r)$ de cada espira y el campo magnético $d\bar{B}(r,z)$ generado por ella en el eje de la espira a una distancia $z$ del disco, podremos integrar lo que hace cada de ellas en un campo total.
Primero repasaremos como determinar el campo magnético generado por una espira en su eje de simetría y luego nos concentraremos en la desafiante tarea de encuntrar la corriente $dI(r)$ de cada espira.
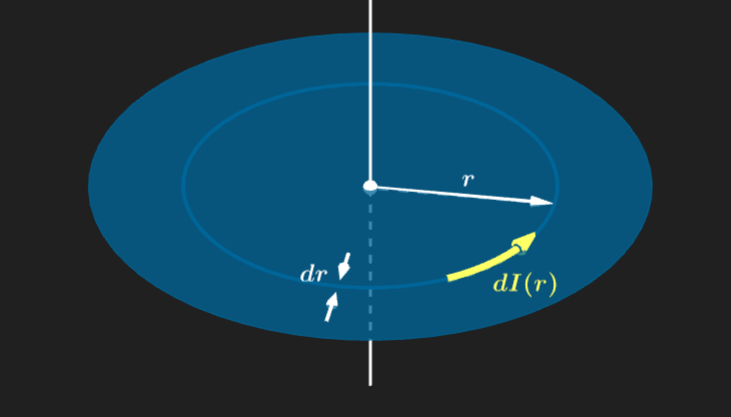
Figura 1
Disco girando a la velocidad angular $\omega$ concebido como un continuo de espiras de corriente $dI(r)$.
Campo magnético de una espira
Consideremos el caso de una espira circular de radio $r$, por la cual circula una corriente $I$. Intentemos determinar el campo magnético en un punto ubicado en su eje de simetría a una distancia $z$ de su eje (Figura 2).
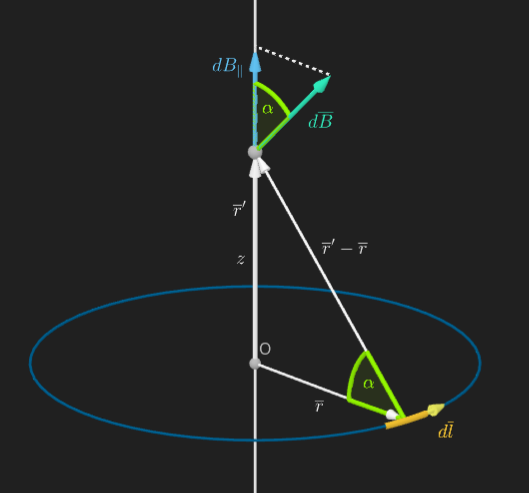
Figura 2
Como es usual, podemos usar la ley de Biot-Savart para calcular el campo magnético buscado. Para ello, aprovecharemos también la simetría del problema: ya que un elemento de corriente $I d \overline{l}$ genera un campo magnético $d \overline{l}$ cuyas componentes perpendiculares al eje se anulan con las componentes del campo producido por un elemento de corriente diametralmente opuesto; así, sólo sobreviven las componentes $ dB_{||}$ paralelas al eje de la espira.
En el contexto de la Figura 2, si elegimos como origen de coordenadas el centro $O$ de la espira, podemos expresar el campo $d \bar{B}$ en el punto $\overline{r}’$ generado por un elemento de corriente $I d \overline{l}$ ubicado en $\overline{r}$:
$$ d\bar{B} = \frac{\mu_{0}}{4\pi } \frac{Id\overline{l}\times (\overline{r}’-\overline{r})}{ ||\overline{r}’-\overline{r}||^{3}}. ~~~~~~\text{(2)}. $$
Si el punto $\overline{r}’$ está ubicado sobre el eje de la espira, la componente $dB_{||}$ paralela al mismo estará dada por
$$ dB_{||}= dB \cos \alpha, ~~~~~~\text{(3)} $$
donde $\alpha$ es el ángulo que subtiende $d \bar{B}$ con el eje de la espira, que a su vez coincide con el angulo que subtienden las direcciones dadas por $\overline{r}$ y $\overline{r}’-\overline{r}$. El módulo del campo $d B$ puede expresarse, teniendo en cuenta la relación (2) como
$$ dB = \frac{\mu _{0}}{4\pi } \frac{Idl}{ ||\overline{r}’-\overline{r}||^{2}}. $$
Como $||\overline{r}’-\overline{r}||^{2} = z^2+r^2$ y $\cos \alpha = r/||\overline{r}’-\overline{r}||$, con el resultado anterior podemos reexpresar la relación (3):
$$ dB_{||} = \frac{\mu_{0}}{4\pi } \frac{r Id l}{ ||\overline{r}’-\overline{r}||^{3}} = \frac{\mu_{0}}{4\pi } \frac{r Idl}{ (z^2+r^2)^{\frac{3}{2}}}. $$
Integrando a lo largo de toda la espira:
$$
\begin{split}
B(z,r) &= \int_{0}^{2 \pi r} d B_{||} \\
&= \int_{0}^{2 \pi r} \frac{\mu_{0}}{4\pi } \frac{r Idl}{ (z^2+r^2)^{\frac{3}{2}}} \\
&= \frac{\mu_{0}}{4\pi } \frac{r I}{ (z^2+r^2)^{\frac{3}{2}}} \int_{0}^{2 \pi r} dl\\
&= \frac{\mu_{0}}{4\pi } \frac{r I}{ (z^2+r^2)^{\frac{3}{2}}} 2 \pi r,
\end{split}
$$
es decir,
$$ B(z,r) = \frac{\mu_{0}}{2 } \frac{r^2 I}{ (z^2+r^2)^{\frac{3}{2}}}. ~~~~~~\text{(4)} $$
Intensidad de corriente elemental
Para determinar la intensidad de corriente de una espira elemental de radio $r$ y espesor $dr$, en un disco cargado con una densidad $\sigma$ (dada por la relación (1)), recurriremos al concepto de densidad de corriente. Como en la bibliografía usual sólo se expone el concepto de densidad de corriente volumétrica y en este ejemplo necesitamos del concepto de densidad de corriente superficial, recordaremos la primera para construir la segunda mediante una analogía.
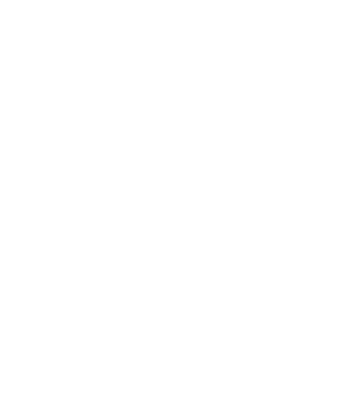
Figura 3
Recordemos como se expresa la intensidad de corriente elemental $dI$ asociada al flujo volumétrico de carga que atraviesa una superficie $d\bar{S}$ a la velocidad $\bar{u}$ en el tiempo $dt$ (Figura 3). La cantidad de carga que atraviesa la superficie está dada por $d q = \rho dV$ donde $\rho$ es la densidad volumétrica de carga y $dV = (\bar{u}dt)\cdot(d\bar{S})= \bar{u} \cdot d\bar{S} dt$ es el volumen que contiene esa cantidad de carga. Así, la intensidad de corriente en la superficie elemental $dS$ es: $$ d I = \left( \frac{dq}{dt} \right)_{dS} = \rho \bar{u} \cdot d\bar{S} $$
De esta última expresión se puede identificar inmediatamente la densidad de corriente $\overline{j}$ definida por la expresión $d I = \bar{j} \cdot d\bar{S}$. En este caso $\bar{j} = \rho \bar{u}$.
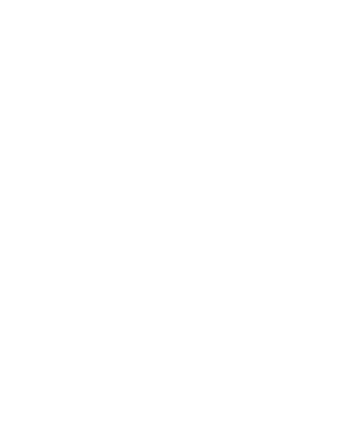
Figura 4
El análisis previo es válido para un flujo volumétrico de carga. Veamos como aprovecharlo para hacer algo que nos sirva para esta ocasión, es decir, para un flujo superficial de carga. Podemos imaginar que pretendemos estudiar la intensidad de corriente elemental $dI$ asociada al flujo superficial de carga que atraviesa un segmento $dr$ a la velocidad $\bar{u}$ en el tiempo $dt$. Llamemos $\theta$ al ángulo que subtiende la velocidad con la dirección perpendicular al segmento $dr$. La cantidad de carga que atraviesa la superficie está dada por $d q = \sigma dS$ donde $\sigma$ es la densidad superficial de carga y $dS = (udt \cos \theta)dr= u \cos \theta dr dt$ es la superficie que contiene esa cantidad de carga. Así, la intensidad de corriente en el segmento elemental $dr$ es:
$$ d I = \left( \frac{dq}{dt} \right)_{dr} = \sigma u \cos \theta dr ~~~~~~\text{(5)} $$
es posible intepretar esta relación, como la definición de una densidad de corriente superficial $\overline{g}$, que tiene la dirección de movimiento y cuyo módulo es $g=\sigma u$. Podemos expresar la corriente elemental como un producto escalar pero para ello será necesario definir un vector perpendicular al segmento $dr$ y cuyo módulo también sea $dr$, llamémosle $d \overline{r}_{\perp}$, entonces
$$ d I = \left( \frac{dq}{dt} \right)_{dr} = \overline{g} \cdot d\overline{r}_{\perp}, $$
con $\overline{g}=\sigma \bar{u}$.
Campo generado por una espira elemental de radio $r$
Si aplicamos lo desarrollado anteriormente a nuestra espira elemental de radio $r$ de sección $dr$ y tenemos en cuenta que la velocidad de movimiento está dada por $u=\omega r$ es perpendicular al segmento $dr$ ($\theta=0$ en la relación (5)):
$$ d I (r) =\sigma u dr = \sigma \omega r dr $$
Por otro lado, interpretando la relación (4) para la espira elemental tendremos un campo elemental dado por $$ dB(z,r) = \frac{\mu_{0}}{2 } \frac{r^2 dI(r)}{ (z^2+r^2)^{\frac{3}{2}}}. $$
es decir,
$$ B(z)= \int_0^R dB(z,r) = \frac{\mu_{0}\sigma \omega}{2} \int_0^R \frac{r^3dr }{ (z^2+r^2)^{\frac{3}{2}}}. $$
Para la integral $\mathcal{I}=\int \frac{r^3dr }{ (z^2+r^2)^{\frac{3}{2}}}$ podemos definir $w= z^2+r^2$ de manera que se puede desarrollar de la siguiente forma:
$$ \begin{split} \mathcal{I} &= \frac{1}{2} \int \frac{(w^2-z^2)dw }{ w^{\frac{3}{2}}}. \\ &= \frac{1}{2} \left[\int \frac{dw}{w^{\frac{1}{2}}} - z^2\int \frac{dw}{w^{\frac{3}{2}}} \right]\\ &= w^{\frac{1}{2}} + \frac{z^2}{w^{\frac{1}{2}}} \\ &= \sqrt{z^2+r^2} + \frac{z^2}{\sqrt{z^2+r^2}} \\ &=\frac{2z^2+r^2}{\sqrt{z^2+r^2}} \end{split} $$
entonces
$$ B(z) = \frac{\mu_{0}\sigma \omega}{2} \left. \left(\frac{2z^2+r^2}{\sqrt{z^2+r^2}}\right) \right|_0^R. $$
y obtenemos lo que nos pidieron inicialmente
$$ \boxed{B(z) =\frac{\mu_{0}\sigma \omega}{2} \left(\frac{2z^2+R^2}{\sqrt{z^2+R^2}} - 2z \right) }. $$
(¡Gooooolazo!)
Si llegaste hasta aquí, gracias! Hago todo esto con muchas ganas y a puro pulmón. Si estas leyendo estas líneas es porque posiblemente estés haciendo un esfuerzo similar. Y eso se agradece. Por otro lado, si queres darme una manito para que pueda dedicarle más tiempo a propuestas como estas podes suscribirte como Colaborador o hacer tu aporte libre y voluntario. ¡Gracias!