N°08-2010

Enunciado

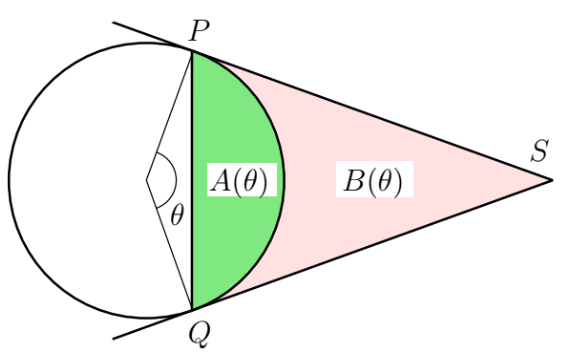
Un arco de circunferencia $\stackrel{\textstyle\frown}{\mathrm{PQ}}$ está subtendido por el ángulo $\theta$, como muestra la figura. Sea $A(\theta)$ el área entre la cuerda $\overline{PQ}$ y el arco $\stackrel{\textstyle\frown}{\mathrm{PQ}}$. Sea $B(\theta)$ el área entre los segmentos tangentes a la circunferencia $\overline{PS}$ y $\overline{QS}$, y el arco $\stackrel{\textstyle\frown}{\mathrm{PQ}}$. Calcular: $$ \lim_{\theta \to 0} \frac{A(\theta)}{B(\theta)} $$

Resolución

Determinación de $A(\theta)$

Determinaremos el área $A(\theta)$ como la diferencia entre el área $S(\theta)$ del sector circular definido por $\theta$ y el área del triangulo $\Delta OPQ$.

1. Área del triangulo $\Delta OPQ$

   Denominemos $r$ al radio de la circunferencia y $O$ a su centro. La base del triangulo $\Delta OPQ$ es $2r \sin(\theta/2)$ y su altura es $r \cos (\theta/2)$, de manera que $$ A(\Delta OPQ) = r^2 \sin(\theta/2) \cos (\theta/2) = \frac{r^2 \sin(\theta)}{2}. $$

2. Área $S(\theta)$ del sector circular definido por $\theta$

   No es difícil recordar que un elemento diferencial de superficie de un sector circular de ángulo $d \theta$ puede considerarse como un triángulo de base $ds= r d \theta$ y altura $r$, de manera que $dS = \frac{r^2 d \theta}{2}$ y por lo tanto

   $$ S (\theta) = \frac{r^2 \theta}{2}. ~~~~~~\text{(1)}. $$

De esta forma, como $A(\theta) = S(\theta) - A(\Delta OPQ)$, $$ A (\theta) = \frac{r^2 }{2} \left[ \theta - \sin(\theta) \right]. ~~~~~~\text{(2)} $$

Cálculo del área $B (\theta)$

Podemos obtener el área $B (\theta)$ a través de la diferencia entre el área $C(OPSQ)$, del trapecio $OPSQ$, con el área del sector circular $S(\theta)$ obtenida en (1). El trapecio $OPSQ$ queda formado por dos triángulos simétricos cuando lo dividimos por el segmento $\overline{OS}$. Nos concentremos en uno de ellos, por ejemplo el triangulo $\Delta OPS$, del cuál podemos tomar como base $OP=r$ y como altura a $PS =r \tan (\theta/2)$, de manera que su área es

$$ A(\Delta OPS) = \frac{r^2\tan (\theta/2)}{2}. $$

Como $C(OPSQ) = 2 A(\Delta OPS) = r^2\tan (\theta/2)$ y $B(\theta) = C(OPQS) - S(\theta)$, recordando la relación (1) tendremos que $$ B (\theta) = \frac{r^2 }{2} \left[ 2 \tan (\theta/2) - \theta \right]. ~~~~~~\text{(3)} $$

Desarrollo del límite

A partir de las relaciones (2) y (3) podemos escribir $$ \lim_{\theta \to 0} \frac{A(\theta)}{B(\theta)} = \lim_{\theta \to 0} \frac{\theta - \sin(\theta)}{2 \tan (\theta/2) - \theta}, $$

el cuál es un límite indeterminado que podemos expresar usando la Regla de l’Hôpital:

$$ \lim_{\theta \to 0} \frac{A(\theta)}{B(\theta)} = \lim_{\theta \to 0} \frac{1 - \cos(\theta)}{ \sec^2(\theta/2) - 1}. ~~~~~~\text{(4)} $$

Ahora podemos reescribir el numerador con usando la siguiente identidad trigonométrica $\cos (\theta) = \cos^2(\theta/2) - \sin^2(\theta/2)$, que podemos reescribirla como $\cos (\theta) = 2 \cos^2(\theta/2)-1$ para desarrollar las expresiones de la siguiente forma y obtener el límite:

$$ \begin{split} \lim_{\theta \to 0} \frac{A(\theta)}{B(\theta)} &= \lim_{\theta \to 0} \frac{2 \left[ 1 - \cos^2(\theta/2) \right]}{ \sec^2(\theta/2) - 1} \\ &= \lim_{\theta \to 0} \frac{2 \left[ 1 - \cos^2(\theta/2) \right]}{ \frac{1}{\cos^2(\theta/2)} - 1} \\ &= \lim_{\theta \to 0} \frac{2 \left[ 1 - \cos^2(\theta/2) \right]\cos^2(\theta/2)}{1 - \cos^2(\theta/2)} \\ &= \lim_{\theta \to 0} 2\cos^2(\theta/2) \\ \Rightarrow & \boxed{\lim_{\theta \to 0} \frac{A(\theta)}{B(\theta)} =2}. \end{split} $$